题目内容
设数列{an}的前n项和Sn=
+
+
+…+
, 且 Sn•Sn+1=
,则n的值为( )
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| n(n+1) |
| 3 |
| 4 |
| A、9 | B、8 | C、7 | D、6 |
考点:数列的求和
专题:等差数列与等比数列
分析:由裂项求和法推导出Sn =
,由此利用Sn•Sn+1=
,能求出结果.
| n |
| n+1 |
| 3 |
| 4 |
解答:
解:∵Sn =
+
+
+…+
=(1-
)+(
-
)+(
-
)+…+(
-
)
=1-
=
,
Sn•Sn+1=
,
∴
•
=
=
,
∴4n=3n+6,解得n=6.
故选:D.
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| n(n+1) |
=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
Sn•Sn+1=
| 3 |
| 4 |
∴
| n |
| n+1 |
| n+1 |
| n+2 |
| n |
| n+2 |
| 3 |
| 4 |
∴4n=3n+6,解得n=6.
故选:D.
点评:本题考查数列的前n项和的求法及应用,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
设a,b∈R,则“(a-b)a2>0”是“a>b”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、非充分非必要条件 |
| D、充要条件 |
在△ABC中,角A、B、C的对边分别是a、b、c.若asinA+csinC-
asinC=bsinB.则角B等于( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设α、β是两个不重合的平面,m、n是两条不重合的直线,则以下结论错误的是( )
| A、若α∥β,m?α,则 m∥β |
| B、若m∥α,m∥β,α∩β=n,则 m∥n |
| C、若m?α,n?α,m∥β,n∥β,则α∥β |
| D、若m∥α,m⊥β,则α⊥β |
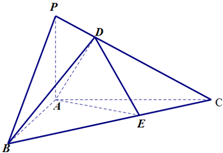 如图,在△ABC中,∠BAC=90°,AC=2AB,PA垂直△ABC所在的平面,PC与△ABC所在的平面成30°角,点D在线段PC上,点E在线段BC上.
如图,在△ABC中,∠BAC=90°,AC=2AB,PA垂直△ABC所在的平面,PC与△ABC所在的平面成30°角,点D在线段PC上,点E在线段BC上.