题目内容
已知一个项数为偶数的等比数列{an}，所有项之和为所有偶数项之和的4倍，前3项之积为64，则a1=（ ）
| A、11 | B、12 | C、13 | D、14 |
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：由已知数据和等比数列的性质可得q的值，由前3项之积为64可得a2，由通项公式可得a1
解答：
解：由题意可得所有项之和S奇+S偶是所有偶数项之和S偶的4倍，
∴S奇+S偶=4S偶，设等比数列{an}的公比为q，
由等比数列的性质可得S偶=qS奇，即S奇=
S偶，
∴
S偶+S偶=4S偶，解得q=
，
又前3项之积a1a2a3=a23=64，解得a2=4，
∴a1=
=12
故选：B
∴S奇+S偶=4S偶，设等比数列{an}的公比为q，
由等比数列的性质可得S偶=qS奇，即S奇=
| 1 |
| q |
∴
| 1 |
| q |
| 1 |
| 3 |
又前3项之积a1a2a3=a23=64，解得a2=4，
∴a1=
| a2 |
| q |
故选：B
点评：本题考查等比数列的通项公式和求和公式，涉及等比数列的性质，属中档题．
练习册系列答案
相关题目
已知m，n表示两条不同直线，α表示平面，下列说法正确的是（ ）
| A、若m∥α，n∥α，则m∥n |
| B、若m⊥α，m⊥n，则n∥α |
| C、若m⊥α，n?α，则m⊥n |
| D、若m∥α，m⊥n，则n⊥α |
将函数y=3sin（2x-
）的图象向左平移
单位得到函数的图象y=f（x），则函数y=f（x）图象的一条对称轴是（ ）
| π |
| 6 |
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
）的图象的第一部分如图所示，则（ ）
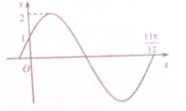
| π |
| 2 |
| A、f（x）的最小正周期为2π | ||
B、f（x）的图象关于直线x=
| ||
C、f（x）的图线关于点（
| ||
D、f（x）在[0，
|