题目内容
求证:
=tan(
+
)
| 1+sinx |
| cosx |
| π |
| 4 |
| x |
| 2 |
考点:三角函数恒等式的证明
专题:证明题,三角函数的求值
分析:由等式的左边开始,运用二倍角的正弦和余弦公式,完全平方公式和平方差公式,结合同角的商数关系,再由两角和的正切公式,即可得到等式的右边.
解答:
证明:
=
=
=
=
=
=tan(
+
),
即有
=tan(
+
).
| 1+sinx |
| cosx |
sin2
| ||||||||
cos2
|
=
(sin
| ||||||||
(cos
|
cos
| ||||
cos
|
=
1+tan
| ||
1-tan
|
tan
| ||||
1-tan
|
| π |
| 4 |
| x |
| 2 |
即有
| 1+sinx |
| cosx |
| π |
| 4 |
| x |
| 2 |
点评:本题考查三角函数的证明,考查二倍角的正弦和余弦公式,考查同角的商数关系和两角和的正切公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知一个项数为偶数的等比数列{an},所有项之和为所有偶数项之和的4倍,前3项之积为64,则a1=( )
| A、11 | B、12 | C、13 | D、14 |
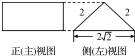 如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8
如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8| 2 |
A、20+8
| ||
B、24+8
| ||
| C、8 | ||
| D、16 |