题目内容
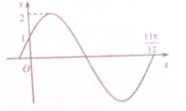
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的图象的第一部分如图所示,则( )
| π |
| 2 |

| A、f(x)的最小正周期为2π | ||
B、f(x)的图象关于直线x=
| ||
C、f(x)的图线关于点(
| ||
D、f(x)在[0,
|
考点:正弦函数的对称性
专题:
分析:由函数的图象的顶点纵坐标求出A,由特殊点求出φ,由五点法作图求出ω的值,可得f(x)的解析式,从而得出结论.
解答:
解:根据函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的图象可得A=2,
把点(0,1)代入求得2sinφ=1,sinφ=
,∴φ=
.
再根据五点法作图可得ω×
+
=2π,解得ω=2,∴f(x)=2sin(2x+
).
当x=
时,f(x)=2sinπ=0,故f(x)的图线关于点(
,0)对称,
故选:C.
| π |
| 2 |
把点(0,1)代入求得2sinφ=1,sinφ=
| 1 |
| 2 |
| π |
| 6 |
再根据五点法作图可得ω×
| 11π |
| 12 |
| π |
| 6 |
| π |
| 6 |
当x=
| 5π |
| 12 |
| 5π |
| 12 |
故选:C.
点评:本题主要考查正弦函数的图象的对称性,由函数y=Asin(ωx+φ)的部分图象求解析式,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知一个项数为偶数的等比数列{an},所有项之和为所有偶数项之和的4倍,前3项之积为64,则a1=( )
| A、11 | B、12 | C、13 | D、14 |
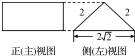 如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8
如图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为8| 2 |
A、20+8
| ||
B、24+8
| ||
| C、8 | ||
| D、16 |