题目内容
过点P(2,1)的直线l与x轴、y轴正方向交于点A、B,分别根据以下条件求直线l的方程:
(1)直线l与x轴、y轴围成等腰三角形;
(2)点P是AB的中点;
(3)S△AOB=6(O为坐标原点);
(4)|OA|+|OB|最小(O为坐标原点).
(1)直线l与x轴、y轴围成等腰三角形;
(2)点P是AB的中点;
(3)S△AOB=6(O为坐标原点);
(4)|OA|+|OB|最小(O为坐标原点).
考点:待定系数法求直线方程
专题:直线与圆
分析:设A(a,0),B(0,b).
(1)由直线l与x轴、y轴围成等腰三角形,则a=b,设直线l的方程为x+y=a,代入P点坐标求得a的值,则直线l的方程可求;
(2)由中点坐标公式列式求得a,b的值代入直线方程的截距式得答案;
(3)设直线l的方程为
+
=1,由
解得a,b的值,则直线方程可求;
(4)由
+
=1,a>0,b>0,得a+b=(a+b)(
+
)展开后利用基本不等式求最值,并得到使a+b最小时的a,b的值,则直线l的方程可求.
(1)由直线l与x轴、y轴围成等腰三角形,则a=b,设直线l的方程为x+y=a,代入P点坐标求得a的值,则直线l的方程可求;
(2)由中点坐标公式列式求得a,b的值代入直线方程的截距式得答案;
(3)设直线l的方程为
| x |
| a |
| y |
| b |
|
(4)由
| 2 |
| a |
| 1 |
| b |
| 2 |
| a |
| 1 |
| b |
解答:
解:如图,
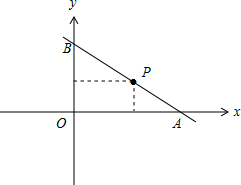
设A(a,0),B(0,b),
(1)直线l与x轴、y轴围成等腰三角形,则a=b,设直线l的方程为x+y=a,
则2+1=a,a=3,
∴直线l的方程为x+y-3=0;
(2)点P是AB的中点,则
,解得a=4,b=2.
∴直线l的方程为
+
=1,即x+2y-4=0;
(3)设直线l的方程为
+
=1,
则
,解得
或
.
∴直线l的方程为
+
=1或
+
=1;
(4)由
+
=1,a>0,b>0,
∴a+b=(a+b)(
+
)=3+
+
≥3+2
=3+2
.
当且仅当
=
,即a=
b,也就是a=2+
,b=
+1时上式等号成立.
此时直线l的方程为
+
=1.

设A(a,0),B(0,b),
(1)直线l与x轴、y轴围成等腰三角形,则a=b,设直线l的方程为x+y=a,
则2+1=a,a=3,
∴直线l的方程为x+y-3=0;
(2)点P是AB的中点,则
|
∴直线l的方程为
| x |
| 4 |
| y |
| 2 |
(3)设直线l的方程为
| x |
| a |
| y |
| b |
则
|
|
|
∴直线l的方程为
| x | ||
6+2
|
| y | ||
3-
|
| x | ||
6-2
|
| y | ||
3+
|
(4)由
| 2 |
| a |
| 1 |
| b |
∴a+b=(a+b)(
| 2 |
| a |
| 1 |
| b |
| 2b |
| a |
| a |
| b |
|
| 2 |
当且仅当
| 2b |
| a |
| a |
| b |
| 2 |
| 2 |
| 2 |
此时直线l的方程为
| x | ||
2+
|
| y | ||
|
点评:本题考查了待定系数法求直线的方程,考查了直线方程的截距式,训练了利用基本不等式求最值,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)=ax+xa(a>0),则下列说法正确的是( )
| A、?a>0,f(x)为偶函数,且在R上单调递增 |
| B、?a>0,f(x)-1为奇函数,且在R上单调递增 |
| C、?a>0,f(x)为奇函数,且在R上单调递减 |
| D、?a>0,f(x)-1为偶函数,且在R上单调递减 |
已知一个项数为偶数的等比数列{an},所有项之和为所有偶数项之和的4倍,前3项之积为64,则a1=( )
| A、11 | B、12 | C、13 | D、14 |