题目内容
若x1，x2为函数f（x）=|log2x|-（
）x的两个零点，则下列结论一定成立的是（ ）
| 1 |
| 2 |
| A、x1x2＞1 |
| B、x1x2＜1 |
| C、x1x2≥1 |
| D、x1x2≤1 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：作出y=|log2x|和y=2-x在R上的图象，可知恰有两个交点，设零点为x1，x2且|log2x1|＞|log2x2|，再结合零点存在定理，可得结论．
解答：
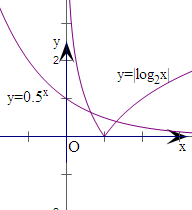解：令f（x）=0，则|log2x|=2-x，
作出y=|log2x|和y=2-x在R上的图象，如图
可知恰有两个函数图形有两个交点，设零点为x1，x2，
且|log2x1|＞|log2x2|，
所以-log2x1＞log2x2，
所以log2
＞log2x2，
故有
＞x2，即x1x2＜1．
故选B．
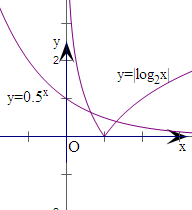解：令f（x）=0，则|log2x|=2-x，作出y=|log2x|和y=2-x在R上的图象，如图
可知恰有两个函数图形有两个交点，设零点为x1，x2，
且|log2x1|＞|log2x2|，
所以-log2x1＞log2x2，
所以log2
| 1 |
| x1 |
故有
| 1 |
| x1 |
故选B．
点评：点评：本题考查函数的零点与方程根的关系，考查数形结合的数学思想，考查学生分析解决问题的能力，正确作出函数图象是关键．
练习册系列答案
相关题目
如图，四边形ABCD为矩形，PD⊥平面ABCD，PD=DC，E是PC的中点．已知椭圆
+
=1（a＞0，b＞0），M，N是椭圆上关于原点对称的两点，P是椭圆上的动点，且直线PM，PN的斜率分别为k1，k2，k1k2≠0，若|k1|+|k2|的最小值为
，则椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设函数y=f（x）在（a，b）上的导函数为f′（x），f′（x）在（a，b）上的导函数为f″（x），若在（a，b）上，f″（x）＜0恒成立，则称函数函数f（x）在（a，b）上为“凸函数”．已知当m≤2时，f（x）=
x3-
mx2+x在（-1，2）上是“凸函数”．则f（c）在（-1，2）上（ ）
| 1 |
| 6 |
| 1 |
| 2 |
| A、既有极大值，也有极小值 |
| B、既有极大值，也有最小值 |
| C、有极大值，没有极小值 |
| D、没有极大值，也没有极小值 |
