题目内容
函数f(x)=2sin(πx)-
,x∈[-2,4]的所有零点之和为 .
| 1 |
| 1-x |
考点:正弦函数的图象
专题:函数的性质及应用
分析:设t=1-x,则x=1-t,原函数可化为g(t)=2sinπt-
,由于g(x)是奇函数,观察函数y=2sinπt与y=
的图象可知,在[-3,3]上,两个函数的图象有8个不同的交点,其横坐标之和为0,从而 x1+x2+…+x7+x8的值.
| 1 |
| t |
| 1 |
| t |
解答:
 解:设t=1-x,则x=1-t,原函数可化为:
解:设t=1-x,则x=1-t,原函数可化为:
g(t)=2sin(π-πt)-
=2sinπt-
,其中,t∈[-3,3],
因g(-t)=-g(t),
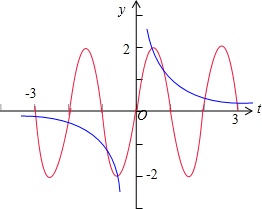
故g(t) 是奇函数,观察函数 y=2sinπt(红色部分)
与曲线y=
(蓝色部分)的图象可知,
在t∈[-3,3]上,两个函数的图象有8个不同的交点,
其横坐标之和为0,即t1+t2+…+t7+t8=0,
从而x1+x2+…+x7+x8=8,
故答案为:8.
 解:设t=1-x,则x=1-t,原函数可化为:
解:设t=1-x,则x=1-t,原函数可化为:g(t)=2sin(π-πt)-
| 1 |
| t |
| 1 |
| t |
因g(-t)=-g(t),
故g(t) 是奇函数,观察函数 y=2sinπt(红色部分)
与曲线y=
| 1 |
| t |
在t∈[-3,3]上,两个函数的图象有8个不同的交点,
其横坐标之和为0,即t1+t2+…+t7+t8=0,
从而x1+x2+…+x7+x8=8,
故答案为:8.
点评:本题主要考查正弦函数的图象特征,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
一个棱锥的三视图如图所示,则这个棱锥的体积为( )


| A、12 | B、36 | C、16 | D、48 |