题目内容
某学校从高三全体500名学生中抽50名学生做学习状况问卷调查，现将500名学生从l到500进行编号，求得间隔数k=
=10，即每10人抽取一个人，在1～10中随机抽取一个数，如果抽到的是6，则从125～140的数中应取的数是 ．
| 500 |
| 50 |
考点：系统抽样方法
专题：概率与统计
分析：根据系统抽样的定义进行计算即可得到结论．
解答：
解：根据系统抽样的定义可知抽取的号码构成以6为首项，公差d=10的等差数列{an}，
∴则an=6+10（n-1）=10n-4，
由125≤10n-4≤140，解得129≤10n≤144，
即12.9≤n≤14.4，
即n=13，或n=14，即两个号码为126和136，
故答案为：126和136
∴则an=6+10（n-1）=10n-4，
由125≤10n-4≤140，解得129≤10n≤144，
即12.9≤n≤14.4，
即n=13，或n=14，即两个号码为126和136，
故答案为：126和136
点评：本题主要考查系统抽样的应用，根据系统抽样转化为等差数列是解决本题的关键，比较基础．
练习册系列答案
相关题目
执行如图所示的程序框图，若输入的p=0.8，则输出的n为（ ）
| A、4 | B、5 | C、6 | D、3 |
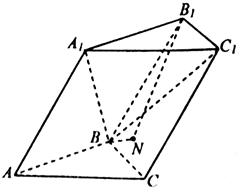如图，三棱柱ABC-A1B1C1中，△ABC是正三角形，AA1=AB=2，平面ACC1A1⊥平面ABC，∠A1AC=60°．下列命题中正确的是（ ）
| A、20.3＞1＞0.32 | ||||
| B、?m，n∈R+，lg（m+n）=lgm•lgn | ||||
C、0.31
| ||||
D、如果a
|