题目内容
设f(x)=|x-a|,a∈R.
(Ⅰ)当-1≤x≤3时,f(x)≤3,求a的取值范围;
(Ⅱ)若对任意的x∈R,f(x-a)+f(x+a)≥1-2a恒成立,求实数a的最小值.
(Ⅰ)当-1≤x≤3时,f(x)≤3,求a的取值范围;
(Ⅱ)若对任意的x∈R,f(x-a)+f(x+a)≥1-2a恒成立,求实数a的最小值.
考点:绝对值不等式的解法,函数恒成立问题
专题:不等式的解法及应用
分析:(Ⅰ)由 f(x)≤3解得a-3≤x≤a+3,由题意可得
,由此解得a的范围.
(Ⅱ)利用基本不等式求得f(x-a)+f(x+a)的最小值为2|a|,结合题意可得2|a|≥1-2a,解得a的范围.
|
(Ⅱ)利用基本不等式求得f(x-a)+f(x+a)的最小值为2|a|,结合题意可得2|a|≥1-2a,解得a的范围.
解答:
解:(Ⅰ) f(x)≤3,即|x-a|≤3,解得a-3≤x≤a+3,
由题意可得
,
解得 0≤a≤2,即a的范围是[0,2].
(Ⅱ)f(x-a)+f(x+a)=|x-2a|+|x|≥|(x-2a)-x|=2|a|,
当且仅当(x-2a)x≤0时,等号成立.
结合题意可得2|a|≥1-2a,
解得a≥
,故a的最小值为
.
由题意可得
|
解得 0≤a≤2,即a的范围是[0,2].
(Ⅱ)f(x-a)+f(x+a)=|x-2a|+|x|≥|(x-2a)-x|=2|a|,
当且仅当(x-2a)x≤0时,等号成立.
结合题意可得2|a|≥1-2a,
解得a≥
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
下列命题中正确的是( )
| A、20.3>1>0.32 | ||||
| B、?m,n∈R+,lg(m+n)=lgm•lgn | ||||
C、0.31
| ||||
D、如果a
|
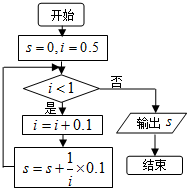
执行如图的程序框图,则输出的S值等于( )

A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
