题目内容
等腰三角形ABC中,AB=AC=4
,∠B=45°,P为线段AB中点,则
•
的值为 .
| 2 |
| CP |
| BC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由已知建立直角坐标系,利用向量的坐标运算和数量积运算即可得出.
解答:
 解:∵AB=AC,∠B=45°,
解:∵AB=AC,∠B=45°,
∴∠ACB=45°,
∴∠A=90°.
如图所示,C(4
,0),A(0,0),B(0,4
),P(0,2
).
∴
=(-4
,2
),
=(4
,-4
).
∴
•
=-4
×4
-2
×4
=-32-16=-48.
故答案为:-48.
 解:∵AB=AC,∠B=45°,
解:∵AB=AC,∠B=45°,∴∠ACB=45°,
∴∠A=90°.
如图所示,C(4
| 2 |
| 2 |
| 2 |
∴
| CP |
| 2 |
| 2 |
| BC |
| 2 |
| 2 |
∴
| CP |
| BC |
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:-48.
点评:本题考查了向量的坐标运算和数量积运算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题中正确的是( )
| A、20.3>1>0.32 | ||||
| B、?m,n∈R+,lg(m+n)=lgm•lgn | ||||
C、0.31
| ||||
D、如果a
|
如图程序输出的结果是( )


| A、3 | B、7 | C、15 | D、19 |
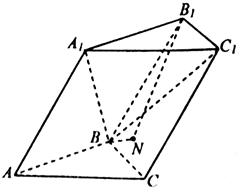 如图,三棱柱ABC-A1B1C1中,△ABC是正三角形,AA1=AB=2,平面ACC1A1⊥平面ABC,∠A1AC=60°.
如图,三棱柱ABC-A1B1C1中,△ABC是正三角形,AA1=AB=2,平面ACC1A1⊥平面ABC,∠A1AC=60°.