题目内容
已知函数f(x)=x2+(a-2)x+a-1,且f(x)在[2,+∞)上单调递增,在(-∞,2]上单调递减.
(1)求实数a的值;
(2)求函数f(x)的最小值;
(3)不等式f(x)≥-2的解.
(1)求实数a的值;
(2)求函数f(x)的最小值;
(3)不等式f(x)≥-2的解.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)利用二次函数的对称轴方程,即可求出实数a的值;
(2)直接利用二次函数的性质求出函数f(x)的最小值;
(3)转化不等式f(x)≥-2为二次不等式,直接求解即可.
(2)直接利用二次函数的性质求出函数f(x)的最小值;
(3)转化不等式f(x)≥-2为二次不等式,直接求解即可.
解答:
解:(1)∵f(x)在[2,+∞)上单调递增,在(-∞,2]上单调递减,
∴函数f(x)=x2+(a-2)x+a-1对称轴为x=-
=2,
∴a=-2,
∴f(x)=x2-4x-3.
(2)∵f(x)=x2-4x-3,
∴当且仅当x=2时,f(x)min=-3-
=-7.
(3)∵f(x)≥-2,
∴x2-4x-3≥-2,即x2-4x-1≥0.
∵x1,2=
=2±
,
∴不等式f(x)≥-2的解集为:(-∞,2-
]∪[2+
,+∞).
∴函数f(x)=x2+(a-2)x+a-1对称轴为x=-
| a-2 |
| 2 |
∴a=-2,
∴f(x)=x2-4x-3.
(2)∵f(x)=x2-4x-3,
∴当且仅当x=2时,f(x)min=-3-
| (-4)2 |
| 4×1 |
(3)∵f(x)≥-2,
∴x2-4x-3≥-2,即x2-4x-1≥0.
∵x1,2=
4±
| ||
| 2 |
| 5 |
∴不等式f(x)≥-2的解集为:(-∞,2-
| 5 |
| 5 |
点评:本题考查二次函数的基本性质,函数的对称轴方程以及函数的最小值,二次不等式的求法,考查计算能力.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
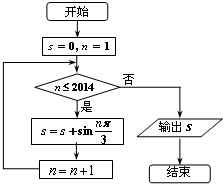
执行如图所示的程序框图,若输入的p=0.8,则输出的n为( )


| A、4 | B、5 | C、6 | D、3 |
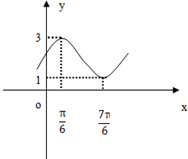 如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象:
如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象: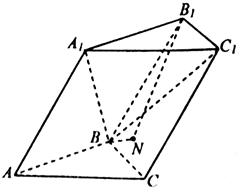 如图,三棱柱ABC-A1B1C1中,△ABC是正三角形,AA1=AB=2,平面ACC1A1⊥平面ABC,∠A1AC=60°.
如图,三棱柱ABC-A1B1C1中,△ABC是正三角形,AA1=AB=2,平面ACC1A1⊥平面ABC,∠A1AC=60°.