题目内容
已知
,
为相互垂直的单位向量,若向量λ
+
与
+λ
的夹角等于60°,则实数λ= .
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:不妨设
、
为直角坐标系中x、y轴上的单位向量,则向量λ
+
=(λ,1),
+λ
=(1,λ).根据向量λ
+
与
+λ
的夹角等于60°,可得cos60°=
,由此求得λ的值.
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| (λ ,1)•(1 ,λ) | ||||
|
解答:
解:∵
,
为相互垂直的单位向量,不妨设
、
直角坐标系中x、y轴上的单位向量,
则向量λ
+
=(λ,1),
+λ
=(1,λ).
∵向量λ
+
与
+λ
的夹角等于60°,则有cos60°=
=
,
解得:λ=2±
,
故答案为:2±
.
| e1 |
| e2 |
| e1 |
| e2 |
则向量λ
| e1 |
| e2 |
| e1 |
| e2 |
∵向量λ
| e1 |
| e2 |
| e1 |
| e2 |
| 1 |
| 2 |
| (λ ,1)•(1 ,λ) | ||||
|
解得:λ=2±
| 3 |
故答案为:2±
| 3 |
点评:本题主要考查用数量积表示两个两个向量的夹角,两个向量的数量积公式,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
执行如图的程序框图.若输入n=7,则输出的值为( )


| A、2 | B、3 | C、4 | D、5 |
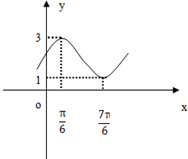 如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象:
如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象: