题目内容
设p：?x∈R，x2+2x-m＞0恒成立；q：方程x2+2（m-2）x-3m+10=0无实根，若p或q为真，p且q为假，则求实数m的取值范围．
考点：复合命题的真假
专题：简易逻辑
分析：首先，分别求解两个命题都是真命题时，实数m的取值情况，然后，结合p或q为真，p且q为假，则两个命题必一真一假，分两种情形进行讨论．
解答：
解：令f（x）=x2+2x-m．
则由△＜0，求得m＜-1，
∴由命题p得：m∈（-∞，-1）．
由命题q得：△=4（m-2）2-4（-3m+10）＜0⇒-2＜m＜3．
由p或q为真，p且q为假知，p、q一真一假．
①当p真q假时，
，即m≤-2；
②当p假q真时，
，即-1≤m＜3．
∴m≤-2或-1≤m＜3．
∴实数m的取值范围（-∞，-2]∪[-1，3）．
则由△＜0，求得m＜-1，
∴由命题p得：m∈（-∞，-1）．
由命题q得：△=4（m-2）2-4（-3m+10）＜0⇒-2＜m＜3．
由p或q为真，p且q为假知，p、q一真一假．
①当p真q假时，
|
②当p假q真时，
|
∴m≤-2或-1≤m＜3．
∴实数m的取值范围（-∞，-2]∪[-1，3）．
点评：本题综合考查了复合命题的应用，方程的根的判断方法、不等式恒成立等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
设复数z=
，则
=（ ）
| 2i |
| 1-i |
. |
| z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
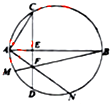如图，AB是⊙O的直径，弦CD与AB垂直，并与AB相交于点E，点F为弦CD上异于点E的任意一点，连接BF、AF并延长交⊙O于点M、N．
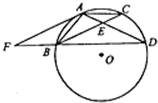如图，点A，B，C，D在⊙O上，AB=AC，AD与BC相交于点E，AE=