题目内容
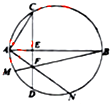如图，AB是⊙O的直径，弦CD与AB垂直，并与AB相交于点E，点F为弦CD上异于点E的任意一点，连接BF、AF并延长交⊙O于点M、N．（1）求证：B、E、F、N四点共圆；
（2）求证：AC2+BF•BM=AB2．
考点：与圆有关的比例线段,圆內接多边形的性质与判定
专题：选作题,立体几何
分析：（1）连结BN，证明∠BEF+∠BNF=180°，即可证明B、E、F、N四点共圆；
（2）由直角三角形的射影原理可知AC2=AE•AB，由Rt△BEF与Rt△BMA相似可知：
=
，即可得出结论．
（2）由直角三角形的射影原理可知AC2=AE•AB，由Rt△BEF与Rt△BMA相似可知：
| BF |
| BA |
| BE |
| BM |
解答：
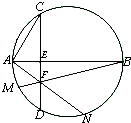证明：（1）连结BN，则AN⊥BN，
又CD⊥AB，
则∠BEF=∠BNF=90°，即∠BEF+∠BNF=180°，
则B、E、F、N四点共圆．…（5分）
（2）由直角三角形的射影原理可知AC2=AE•AB，
由Rt△BEF与Rt△BMA相似可知：
=
，
∴BF•BM=BA•BE=BA•（BA-EA），
∴BF•BM=AB2-AB•AE，
∴BF•BM=AB2-AC2，即AC2+BF•BM=AB2．…（10分）
证明：（1）连结BN，则AN⊥BN，又CD⊥AB，
则∠BEF=∠BNF=90°，即∠BEF+∠BNF=180°，
则B、E、F、N四点共圆．…（5分）
（2）由直角三角形的射影原理可知AC2=AE•AB，
由Rt△BEF与Rt△BMA相似可知：
| BF |
| BA |
| BE |
| BM |
∴BF•BM=BA•BE=BA•（BA-EA），
∴BF•BM=AB2-AB•AE，
∴BF•BM=AB2-AC2，即AC2+BF•BM=AB2．…（10分）
点评：本题考查四点共圆，考查三角形相似，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
某校高三年级从一次模拟考试中随机抽取50名学生（男、女生各25名），将数学成绩进行统计，所得数据的茎叶图如图所示，以组距为10将数据按[80，90），[90，100），…，[130，140），[140，150]分成七组绘制频率分布直方图，则落在区间[130，140）的小矩形的面积为（ ）