Question

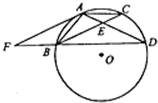如图，点A，B，C，D在⊙O上，AB=AC，AD与BC相交于点E，AE=

1

2

ED，延长DB到点F，使FB=

1

2

BD，连结AF．求证：
（Ⅰ）△BDE∽△FDA；
（Ⅱ）FA²=FB•FD．

Answer 1

考点：与圆有关的比例线段,相似三角形的判定

专题：选作题,立体几何

分析：（Ⅰ）利用AE=

1

2

ED，FB=

1

2

BD，可得

DE

DA

=

DB

DF

=

2

3

，利用∠EDB=∠ADF，可得△BDE∽△FDA；
（Ⅱ）证明OA⊥FA，可得直线AF与⊙O相切，即可证明FA²=FB•FD．

解答： 证明：（Ⅰ）在△BDE和△FDA中，
∵AE=

1

2

ED，FB=

1

2

BD，
∴

DE

DA

=

DB

DF

=

2

3

，
∵∠EDB=∠ADF，
∴△BDE∽△FDA；
（Ⅱ）连OA，OB，OC，则
∵AB=AC，
∴∠BOA=∠COA，
∵OB=OC，
∴OA⊥BC，
∵△BDE∽△FDA，
∴∠EBD=∠AFD，
∴BC∥FA，
∵OA⊥BC，
∴OA⊥FA，
∴直线AF与⊙O相切，
∴FA²=FB•FD．

点评：本题考查了切线的判定定理：过半径的外端点与半径垂直的直线是圆的切线．也考查了垂径定理的推论以及平行线分线段成比例定理．