题目内容
f(x)为R上的偶函数,且当x∈(-∞,0)时,f(x)=x(x-1),则当x∈(0,+∞)时,f(x)= .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:首先,根据x∈(0,+∞),得到-x∈(-∞,0),然后,借助于已知的解析式进行求解.
解答:
解:∵x∈(0,+∞),
∴-x∈(-∞,0),
∴f(-x)=-x(-x-1)=x(x+1),
∵f(x)为R上的偶函数,
∴f(-x)=f(x),
∴f(x)=x(x+1),
∴当x∈(0,+∞)时,f(x)=x(x+1),
故答案为:x(x+1).
∴-x∈(-∞,0),
∴f(-x)=-x(-x-1)=x(x+1),
∵f(x)为R上的偶函数,
∴f(-x)=f(x),
∴f(x)=x(x+1),
∴当x∈(0,+∞)时,f(x)=x(x+1),
故答案为:x(x+1).
点评:本题重点考查了偶函数的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)(x∈R)的图象上任一点(x0,y0)处切线的方程为:y-y0=(x0-2)( x0-1)(x-x0),那么函数f(x)的单调减区间是( )
| A、(1,2) |
| B、(-∞,1] |
| C、[2,+∞) |
| D、(-∞,-1) |
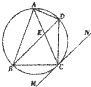 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=