题目内容
对于满足a+b=4的所有实数a，b，则直线3ax+2y-7b=（b-1）y必过定点 ．
考点：恒过定点的直线
专题：计算题,直线与圆
分析：由条件a+b=4，化简直线（12x+3y）-b（3x+y+7）=0，为经过定点的直线系，求出定点坐标．
解答：
解：直线3ax+2y-7b=（b-1）y．由条件a+b=4，可得3（4-b）x+2y-7b=（b-1）y．
可得（12x+3y）-b（3x+y+7）=0，
∵b∈R，∴
，解得x=7，y=-28，
故直线3ax+2y-7b=（b-1）y过定点（7，-28），
故答案为：（7，-28）．
可得（12x+3y）-b（3x+y+7）=0，
∵b∈R，∴
|
故直线3ax+2y-7b=（b-1）y过定点（7，-28），
故答案为：（7，-28）．
点评：本题主要考查经过定点的直线，考查计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
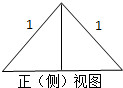如图，是一个四棱锥正视图（主视图）和侧视图（左视图）为两个完全相同的等腰直角三角形，其腰长为1，则该四棱锥的体积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
双曲线
-
=1（a＞0，b＞0）的一个焦点与抛物线y2=16x的焦点重合，且双曲线
-
=1上有一点到一个焦点的距离比到另一焦点的距离大4，则（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、b=4 | ||
B、b=2
| ||
C、b=4
| ||
D、b=2
|