题目内容
若将函数f（x）=x4表示为f（x）=a0+a1（1+x）+a2（1+x）2+a3（1+x）3+a4（1+x）4其中a0，a1，a2，a3，a4为实数，则a2= ．
考点：二项式系数的性质
专题：计算题,二项式定理
分析：根据[-1+（1+x）]4=a0+a1（1+x）+a2（1+x）2+a3（1+x）3+a4（1+x）4 ，利用展开式的通项公式求出a2的值．
解答：
解：由题意可得[-1+（1+x）]4=a0+a1（1+x）+a2（1+x）2+a3（1+x）3+a4（1+x）4，
∴a2=
×（-1）2=6，
故答案为：6
∴a2=
| C | 2 4 |
故答案为：6
点评：本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于基础题．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知双曲线
-
=1（a＞0，b＞0）的右顶点和右焦点分别为A（a，0）、F（c，0），若直线x=
上存在点P使得∠APF=30°，则刻双曲线的离心率的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
A、（1，
| ||||
B、[
| ||||
| C、（1，2] | ||||
| D、[2，+∞） |
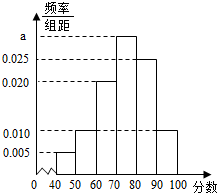从某校高三年级学生中抽取40名学生，将他们高中学业水平考试的数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]后得到如图的频率分布直方图．