题目内容

4．已知实数x，y满足$\left\{{\begin{array}{l}{x-y-1≥0}\\{x+y-3≥0}\\{y≤3}\end{array}}\right.$则2x+y的最小值为（　　）
A．11B．3C．4D．2

分析 画出可行域，设z=2x+y，利用目标函数的几何意义其最小值．

解答 解：由已知得到平面区域如图：设z=2x+y，则y=-2x+z，
由它在y轴的截距最小，得到z最小，
由图可知当直线过A（0，3）时，z 最小，所以最小值为3；
故选：B．

点评 本题考查了简单线性规划问题；只要正确画出可行域，利用目标函数的几何意义求最值即可．

练习册系列答案
相关题目
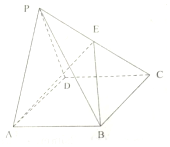14．如图，在四棱锥P-ABCD中，E是PC的中点，底面ABCD为矩形，AB=4，AD=2，△PAD为正三角形，且平面PAD⊥平面ABCD，平面ABE与棱PD交于点F，平面PCD与平面PAB交于直线l．
（1）求证：l∥EF；
（2）求三棱锥P-AEF的体积．
15．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=2$\sqrt{3}$，$\overrightarrow{a}$•$\overrightarrow{b}$=2，则|$\overrightarrow{a}$-$\overrightarrow{b}$|=（　　）
A．8B．4C．2D．1
12．已知过点A（0，1）的椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1、F2，B为椭圆上的任意一点，且$\sqrt{3}$|BF1|，|F1F2|，$\sqrt{3}$|BF2|成等差数列．
（1）求椭圆C的标准方程；
（2）直线l：y=k（x+2）交椭圆于P，Q两点，若点A始终在以PQ为直径的圆外，求实数k的取值范围．
19．若函数f（x）=sin（ωx）（ω＞0）在$[{\frac{π}{4}，\frac{π}{2}}]$上为减函数，则ω的取值范围为（　　）
A．（0，3]B．（0，4]C．[2，3]D．[2，+∞）
9．已知复数$z=\frac{1-i}{i}$，则|z|=$\sqrt{2}$．
16．已知函数f（x）=eax-x．
（Ⅰ）若曲线y=f（x）在（0，f（0））处的切线l与直线x+2y+3=0垂直，求a的值；
（Ⅱ）当a≠1时，求证：存在实数x0使f（x0）＜1．
13．已知函数f（x）=$\frac{1}{3}{x^3}+\frac{1}{2}{x^2}$-2x+1．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）当0＜a≤$\frac{5}{2}$时，求函数f（x）在区间[-a，a]上的最大值．
14．若实数x，y，z满足4x+3y+12z=1，求x2+y2+z2的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网