题目内容
14.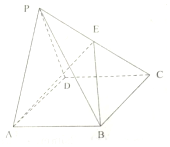 如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.
如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.(1)求证:l∥EF;
(2)求三棱锥P-AEF的体积.
分析 (1)作EF∥CD交PD于F,则利用线面平行的性质证明AB∥l,再利用平行公理得出AB∥EF即可得出结论;
(2)由面面垂直可证EF⊥平面PAD,则VP-AEF=VE-PAF=$\frac{1}{3}{S}_{△PAF}•EF$.
解答 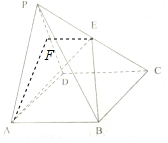 证明:(1)过F作EF∥CD交PD于F,连接EF,AF,
证明:(1)过F作EF∥CD交PD于F,连接EF,AF,
∵E是PC的中点,∴F是PD的中点,
又CD∥AB,
∴EF∥AB,
∵AB∥CD,CD?平面PAC,AB?平面PCD,
∴AB∥平面PCD,又AB?平面PAB,平面PAB∩平面PCD=l,
∴AB∥l,
∴l∥EF.
解:(2)∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,AD⊥CD,
∴CD⊥平面PAD,又CD∥EF,
∴EF⊥平面PAD,
∵底面ABCD为矩形,△PAD为正三角形,AD=2,AB=4,
∴EF=$\frac{1}{2}$CD=$\frac{1}{2}$AB=2,S△PAF=$\frac{1}{2}$S△PAD=$\frac{1}{2}×\frac{\sqrt{3}}{4}×4$=$\frac{\sqrt{3}}{2}$,
∴VP-AEF=VE-PAF=$\frac{1}{3}{S}_{△PAF}•EF$=$\frac{1}{3}×\frac{\sqrt{3}}{2}×2$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了线面平行的性质与判断,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
5.表是一个容量为10的样本数据分组后的频率分布,若利用组中中近似计算本组数据的平均数$\overline x$,则$\overline x$的值为19.7
| 数据 | [12,5,15.5) | [15.5,18.5) | [18.5,21.5) | [21,5,24.5) |
| 频数 | 2 | 1 | 3 | 4 |
6.已知公差不为0的等差数列{an}与等比数列$\{{b_n}\},{a_1}=2,{b_n}={a_{2^n}}$,则{bn}的前5项的和为( )
| A. | 142 | B. | 124 | C. | 128 | D. | 144 |
3.已知函数f(x)=1n(x+2)+1n(x-2),则f(x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
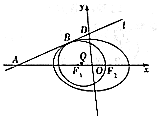 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点A(-4,0)的直线l与椭圆C相切于点B,与y轴交于点D(0,2),又椭圆的离心率为$\frac{1}{2}$.