题目内容
15.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=2$\sqrt{3}$,$\overrightarrow{a}$•$\overrightarrow{b}$=2,则|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
分析 根据数量积的运算可得到$(\overrightarrow{a}-\overrightarrow{b})^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}-4\overrightarrow{a}•\overrightarrow{b}$,进而求出$(\overrightarrow{a}-\overrightarrow{b})^{2}$的值,从而得出$|\overrightarrow{a}-\overrightarrow{b}|$的值.
解答 解:$(\overrightarrow{a}-\overrightarrow{b})^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}-4\overrightarrow{a}•\overrightarrow{b}$
=$(2\sqrt{3})^{2}-4×2$
=4;
∴$|\overrightarrow{a}-\overrightarrow{b}|=2$.
故选C.
点评 考查数量积的运算,求$|\overrightarrow{a}-\overrightarrow{b}|$而求$(\overrightarrow{a}-\overrightarrow{b})^{2}$的方法.

练习册系列答案
相关题目
5.表是一个容量为10的样本数据分组后的频率分布,若利用组中中近似计算本组数据的平均数$\overline x$,则$\overline x$的值为19.7
| 数据 | [12,5,15.5) | [15.5,18.5) | [18.5,21.5) | [21,5,24.5) |
| 频数 | 2 | 1 | 3 | 4 |
6.已知公差不为0的等差数列{an}与等比数列$\{{b_n}\},{a_1}=2,{b_n}={a_{2^n}}$,则{bn}的前5项的和为( )
| A. | 142 | B. | 124 | C. | 128 | D. | 144 |
3.已知函数f(x)=1n(x+2)+1n(x-2),则f(x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
20.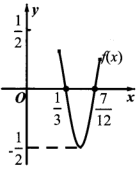 函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
 函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )| A. | $(-\frac{1}{24}+2kπ,\frac{5}{24}+2kπ)$,(k∈Z) | B. | $(-\frac{1}{12}+\frac{k}{2},\frac{5}{12}+\frac{k}{2})$,(k∈Z) | ||
| C. | $(-\frac{1}{12}+2kπ,\frac{1}{3}+2kπ)$,(k∈Z) | D. | $(-\frac{1}{24}+\frac{k}{2},\frac{5}{24}+\frac{k}{2})$,(k∈Z) |
7.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{2}-|x-\frac{3}{2}|(x≤2)}\\{{e}^{x-2}(-{x}^{2}+8x-12)(x>2)}\end{array}\right.$,若在区间(1,∞)上存在n(n≥2)个不同的数x1,x2,x3,…,xn,使得$\frac{f({x}_{1})}{{x}_{1}}$=$\frac{f({x}_{2})}{{x}_{2}}$=…$\frac{f({x}_{n})}{{x}_{n}}$成立,则n的取值集合是( )
| A. | {2,3,4,5} | B. | {2,3} | C. | {2,3,5} | D. | {2,3,4} |