题目内容
12.已知过点A(0,1)的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,B为椭圆上的任意一点,且$\sqrt{3}$|BF1|,|F1F2|,$\sqrt{3}$|BF2|成等差数列.(1)求椭圆C的标准方程;
(2)直线l:y=k(x+2)交椭圆于P,Q两点,若点A始终在以PQ为直径的圆外,求实数k的取值范围.
分析 (1)由题意,利用等差数列和椭圆的定义求出a、c的关系,再根据椭圆C过点A,求出a、b的值,即可写出椭圆C的标准方程;
(2)设P(x1,y1),Q(x2,y2),根据题意知x1=-2,y1=0;联立方程$\left\{\begin{array}{l}{y=k(x+2)}\\{\frac{{x}^{2}}{4}{+y}^{2}=1}\end{array}\right.$消去y,由方程的根与系数关系求得x2、y2,由点A在以PQ为直径的圆外,得∠PAQ为锐角,$\overrightarrow{AP}$•$\overrightarrow{AQ}$>0;由此列不等式求出k的取值范围.
解答 解:(1)∵$\sqrt{3}$|BF1|,|F1F2|,$\sqrt{3}$|BF2|成等差数列,
∴2|F1F2|=$\sqrt{3}$|BF1|+$\sqrt{3}$|BF2|=$\sqrt{3}$(|BF1|+|BF2|),
由椭圆定义得2•2c=$\sqrt{3}$•2a,
∴c=$\frac{\sqrt{3}}{2}$a;
又椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A(0,1),
∴b=1;
∴c2=a2-b2=a2-1=$\frac{3}{4}$a2,
解得a=2,c=$\sqrt{3}$;
∴椭圆C的标准方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)设P(x1,y1),Q(x2,y2)
联立方程$\left\{\begin{array}{l}{y=k(x+2)}\\{\frac{{x}^{2}}{4}{+y}^{2}=1}\end{array}\right.$,消去y得:
(1+4k2)x2+16k2x+(16k2-4)=0;
依题意直线l:y=k(x+2)恒过点(-2,0),此点为椭圆的左顶点,
∴x1=-2,y1=0,----①
由方程的根与系数关系可得,x1+x2=$\frac{-1{6k}^{2}}{1+{4k}^{2}}$;-------②
可得y1+y2=k(x1+2)+k(x2+2)=k(x1+x2)+4k;----③
由①②③,解得x2=$\frac{2-{8k}^{2}}{1+{4k}^{2}}$,y2=$\frac{4k}{1+{4k}^{2}}$;
由点A在以PQ为直径的圆外,得∠PAQ为锐角,即$\overrightarrow{AP}$•$\overrightarrow{AQ}$>0;
由$\overrightarrow{AP}$=(-2,-1),$\overrightarrow{AQ}$=(x2,y2-1),
∴$\overrightarrow{AP}$•$\overrightarrow{AQ}$=-2x2-y2+1>0;
即$\frac{4-1{6k}^{2}}{1+{4k}^{2}}$+$\frac{4k}{1+{4k}^{2}}$-1<0,
整理得,20k2-4k-3>0,
解得:k<-$\frac{3}{10}$或k>$\frac{1}{2}$,
∴实数k的取值范围是k<-$\frac{3}{10}$或k>$\frac{1}{2}$.
点评 本题主要考查椭圆的定义,直线与椭圆的位置关系等基础知识,考查运算求解能力,推理论证能力,考查了函数与方程思想,数形结合思想,化归与转化思想,训练了利用平面向量数量积求解几何问题,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
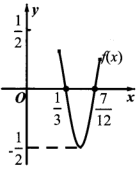 函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )| A. | $(-\frac{1}{24}+2kπ,\frac{5}{24}+2kπ)$,(k∈Z) | B. | $(-\frac{1}{12}+\frac{k}{2},\frac{5}{12}+\frac{k}{2})$,(k∈Z) | ||
| C. | $(-\frac{1}{12}+2kπ,\frac{1}{3}+2kπ)$,(k∈Z) | D. | $(-\frac{1}{24}+\frac{k}{2},\frac{5}{24}+\frac{k}{2})$,(k∈Z) |
| A. | {2,3,4,5} | B. | {2,3} | C. | {2,3,5} | D. | {2,3,4} |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 2 |
| A. | 11 | B. | 3 | C. | 4 | D. | 2 |

| A. | S=-12 | B. | S=-11 | C. | S=-10 | D. | S=-6 |