题目内容
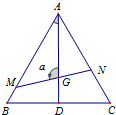如图，△ABC是边长为1的正三角形，M，N分别是边AB，AC上的点，线段MN过△ABC的重心G，设∠MGA=α，α∈[| π |
| 3 |
| 2π |
| 3 |
（1）当α=105°时，求MG的长；
（2）分别记△AGM，△AGN的面积为S1，S2，试将S1，S2表示为α的函数；
（3）求y=
| 1 |
| S12 |
| 1 |
| S22 |
考点：正弦定理,余弦定理
专题：解三角形
分析：（1）根据重心的性质求得AG，利用正弦定理求得MG．
（2）利用正弦定理表示出MG，NG，进而根据三角形面积公式求得S1，S2关于α的函数；
（3）利用（2）中结论，用α表示出y的函数解析式，利用α的范围求得其最大和最小值．
（2）利用正弦定理表示出MG，NG，进而根据三角形面积公式求得S1，S2关于α的函数；
（3）利用（2）中结论，用α表示出y的函数解析式，利用α的范围求得其最大和最小值．
解答：
解：（1）∵，△ABC是边长为1的正三角形，G为重心，
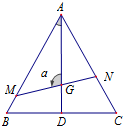
∴AG=
AD=
在△AMG中∠MGA=105°，∠MAG=30°，
∴∠AMG=45°
由正弦定理得
=
∴MG=
•sin30°=
，
（2）∵在△AMG中，∠MAG=30°，
∴∠AMG=150°-α，
由正弦定理得 MG=
sin300=
在△ANG中，同理可得NG=
sin300=
∴S1=
AG•MG•sinα=
α∈[
，
]
∴S1=
AG•NG•sinα=
α∈[
，
]
（3）y=
+
=
+
=
+
=
=
=
+144
∵α∈[
，
]
∴当α=
，ymin=216
当α=
或
，ymax=240
∴AG=
| 2 |
| 3 |
| ||
| 3 |
在△AMG中∠MGA=105°，∠MAG=30°，
∴∠AMG=45°
由正弦定理得
| MG |
| sin30° |
| AG |
| sin45° |
∴MG=
| AG |
| sin45° |
| ||
| 6 |
（2）∵在△AMG中，∠MAG=30°，
∴∠AMG=150°-α，
由正弦定理得 MG=
| AG |
| sin(1500-α) |
| ||
| 6sin(1500-α) |
在△ANG中，同理可得NG=
| AG |
| sin(α-300) |
| ||
| 6sin(α-300) |
∴S1=
| 1 |
| 2 |
| sinα |
| 12sin(1500-α) |
| π |
| 3 |
| 2π |
| 3 |
∴S1=
| 1 |
| 2 |
| sinα |
| 12sin(α-300) |
| π |
| 3 |
| 2π |
| 3 |
（3）y=
| 1 |
| S12 |
| 1 |
| S22 |
| 144sin2(1500-α) |
| sin2α |
| 144sin2(α-300) |
| sin2α |
=
| 72[1-cos(3000-2α)] |
| sin2α |
| 72[1-cos(2α-600)] |
| sin2α |
=
| 72(2-cos2α) |
| sin2α |
| 144-72(1-2sin2α) |
| sin2α |
| 72 |
| sin2α |
∵α∈[
| π |
| 3 |
| 2π |
| 3 |
∴当α=
| π |
| 2 |
当α=
| π |
| 3 |
| 2π |
| 3 |
点评：本题主要考查了正弦定理的应用，三角函数图象和性质等知识点．
练习册系列答案
相关题目
假设a1，a2，a3，a4是一个等差数列，且满足0＜a1＜2，a3=4．若bn=2an（n=1，2，3，4）．给出以下命题：
①数列{bn}是等比数列；
②b2＞4；
③b4＞32；
④b2b4=256．
其中正确命题的个数是（ ）
①数列{bn}是等比数列；
②b2＞4；
③b4＞32；
④b2b4=256．
其中正确命题的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
在△ABC中，已知a=1，b=
，A=30°，B为锐角，那么角A，B，C的大小关系为（ ）
| 3 |
| A、A．＞B＞C |
| B、B＞A＞C |
| C、C＞B＞A |
| D、C＞A＞B |
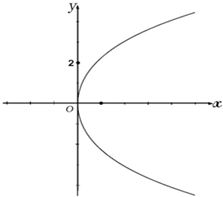已知曲线Γ：y2=4x，直线l经过点（0，2）且其一个方向向量为
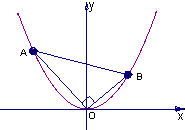在平面直角坐标系xOy中，抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO