题目内容
已知[x]表示不超过实数x的最大整数(x∈R),如:[-1,3]=-2,[0,8]=0,[3,4]=3.定义{x}=x-[x],给出如下命题:
①使[x+1]=3成立的x的取值范围是2≤x<3;
②函数y={x}的定义域为R,值域为[0,1];
③{
}+{
}+{
}+…+{
}=1007;
④设函数f(x)=
,则函数y=f(x)-
x-
的不同零点有3个.
其中正确的命题有( )
①使[x+1]=3成立的x的取值范围是2≤x<3;
②函数y={x}的定义域为R,值域为[0,1];
③{
| 2013 |
| 2014 |
| 20132 |
| 2014 |
| 20133 |
| 2014 |
| 20132014 |
| 2014 |
④设函数f(x)=
|
| 1 |
| 4 |
| 1 |
| 4 |
其中正确的命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:新定义,函数的性质及应用
分析:①由[x]表示不超过实数x的最大整数,即可判断[x+1]=3的x的取值范围;
②函数{x}的定义域为R,推出函数的最小正周期为1,再推出当0≤x<1时,y={x}的值域,从而判断②;
③推出n分别为偶数、奇数时,{
}=
或1-
,从而判断③的正确性;
④可先求出0≤x<3,-3≤x<0的f(x)的表达式,令y=0,则f(x)=
x+
,然后在同一个坐标系中,画出函数y=f(x)和y=
x+
的图象,找出交点个数即可.
②函数{x}的定义域为R,推出函数的最小正周期为1,再推出当0≤x<1时,y={x}的值域,从而判断②;
③推出n分别为偶数、奇数时,{
| 2013n |
| 2014 |
| 1 |
| 2014 |
| 1 |
| 2014 |
④可先求出0≤x<3,-3≤x<0的f(x)的表达式,令y=0,则f(x)=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:①已知[x]表示不超过实数x的最大整数,由[x+1]=3得3≤x+1<4即2≤x<3,故①正确;
②函数{x}的定义域为R,又由{x+1}=(x+1)-[x+1]=x-[x]={x},故函数{x}=x-[x]是周期为1的函数,
当0≤x<1时,{x}=x-[x]=x-0=x,故函数{x}的值域为[0,1),故②错误;
③当n为偶数时,{
}={
}={2014n-1-n•2014n-2+…-n+
}=
,
当n为奇数时,{
}={
}={2014n-1-n•2014n-2+…+n-
}=1-
,
故{
}+{
}+{
}+…+{
}=(
+
)+(
+
)+…+
(
+
)=1007,故③正确;
④当0≤x<1时,f(x)=x-[x]=x-0=x,当1≤x<2,则f(x)=x-1 ,
,
当2≤x<3,则f(x)=x-2,…
当-1≤x<0,则0≤x+1<1,则f(x)=f(x+1)=x+1,
当-2≤x<-1,则-1≤x+1<0,则f(x)=f(x+1)=x+2,
当-3≤x<-2,则-2≤x+1<-1,则f(x)=f(x+1)=x+3,…
令y=0,则f(x)=
x+
,在同一个坐标系中,画出函数y=f(x)和
y=
x+
的图象,显然有3个交点,故④正确.
故选C.
②函数{x}的定义域为R,又由{x+1}=(x+1)-[x+1]=x-[x]={x},故函数{x}=x-[x]是周期为1的函数,
当0≤x<1时,{x}=x-[x]=x-0=x,故函数{x}的值域为[0,1),故②错误;
③当n为偶数时,{
| 2013n |
| 2014 |
| (2014-1)n |
| 2014 |
| 1 |
| 2014 |
| 1 |
| 2014 |
当n为奇数时,{
| 2013n |
| 2014 |
| (2014-1)n |
| 2014 |
| 1 |
| 2014 |
| 1 |
| 2014 |
故{
| 2013 |
| 2014 |
| 20132 |
| 2014 |
| 20133 |
| 2014 |
| 20132014 |
| 2014 |
| 2013 |
| 2014 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
| 1 |
| 2014 |
(
| 2013 |
| 2014 |
| 1 |
| 2014 |
④当0≤x<1时,f(x)=x-[x]=x-0=x,当1≤x<2,则f(x)=x-1
 ,
,当2≤x<3,则f(x)=x-2,…
当-1≤x<0,则0≤x+1<1,则f(x)=f(x+1)=x+1,
当-2≤x<-1,则-1≤x+1<0,则f(x)=f(x+1)=x+2,
当-3≤x<-2,则-2≤x+1<-1,则f(x)=f(x+1)=x+3,…
令y=0,则f(x)=
| 1 |
| 4 |
| 1 |
| 4 |
y=
| 1 |
| 4 |
| 1 |
| 4 |
故选C.
点评:本题是新定义题,考查函数的性质及应用,考查函数的定义域、值域以及函数的周期性,运用图象相交的交点个数来确定函数的零点个数,对定义的准确理解是迅速解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知sin2α=
,则cos2(α-
)=( )
| 1 |
| 3 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
不等式|x-2|<1的解集为( )
| A、[1,3] |
| B、(1,3) |
| C、[-3,-1] |
| D、(-3,-1) |
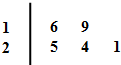 学校为了了解学生每个月在校期间参加体育锻炼的时间,从某班选取5名学生进行调查,他们参加体育锻炼的时间用茎叶图记录如图所示(单位:小时),则这组数据的中位数和方差分别是( )
学校为了了解学生每个月在校期间参加体育锻炼的时间,从某班选取5名学生进行调查,他们参加体育锻炼的时间用茎叶图记录如图所示(单位:小时),则这组数据的中位数和方差分别是( )| A、21和10.8 |
| B、24和10.8 |
| C、25和9.2 |
| D、5和9.2 |
假设a1,a2,a3,a4是一个等差数列,且满足0<a1<2,a3=4.若bn=2an(n=1,2,3,4).给出以下命题:
①数列{bn}是等比数列;
②b2>4;
③b4>32;
④b2b4=256.
其中正确命题的个数是( )
①数列{bn}是等比数列;
②b2>4;
③b4>32;
④b2b4=256.
其中正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
执行如图所示的程序框图,如输入的p=20,则输出的n的值是( )


| A、3 | B、4 | C、5 | D、6 |
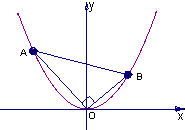 在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO
在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO