题目内容
已知数列{an}满足a1=1，an+1=an+3，则a1+a2+a3+…+a10=（ ）
| A、130 | B、145 |
| C、160 | D、165 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由an+1=an+3可得数列{an}是等差数列，利用等差数列的前n项和公式即可得到结论．
解答：
解：∵数列{an}满足a1=1，an+1=an+3，
∴{an}是等差数列，公差d=3，
则a1+a2+a3+…+a10=10+
×3=10+135=145，
故选：B．
∴{an}是等差数列，公差d=3，
则a1+a2+a3+…+a10=10+
| 10×9 |
| 2 |
故选：B．
点评：本题主要考查等差数列的前n项和的计算，利用条件判断数列{an}是等差数列是解决本题关键．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
已知双曲线
-
=1的焦点到一条渐近线的距离为1，则该双曲线的离心率为（ ）
| x2 |
| 3 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若抛物线y=ax2的焦点为F（0，1），则a的值为（ ）
A、
| ||
| B、4 | ||
C、
| ||
| D、2 |
设某种产品分两道工序生产，第一道工序的次品率为10%，第二道工序的次品率为3%．生产这种产品只要有一道工序出次品就出次品，则该产品的次品率是（ ）
| A、0.13 | B、0.03 |
| C、0.127 | D、0.873 |
已知双曲线的一个焦点坐标为（
，0），且经过点（-5，2），则双曲线的标准方程为（ ）
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若数列{an}的前n项和Sn满足Sn=4-an（n∈N*），则a5=（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
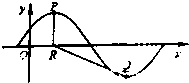已知函数f（x）=Asin（
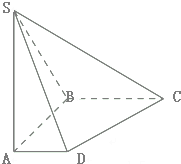如图，已知在四棱锥S-ABCD中，底面四边形ABCD是直角梯形，∠ABC=90°，SA⊥平面ABCD，SA=AB=BC=2．