题目内容
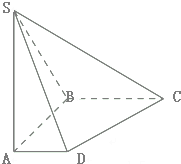 如图,已知在四棱锥S-ABCD中,底面四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=2.
如图,已知在四棱锥S-ABCD中,底面四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=2.(Ⅰ)求证:平面SAB⊥平面SBC;
(Ⅱ)求直线SC与底面ABCD所成角的正切值.
考点:平面与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(Ⅰ)由SA⊥平面ABCD,BC⊆平面ABCD推断出SA⊥BC,又∠ABC=90°即AB⊥BC,利用线面垂直的判定定理推断出BC⊥面SAB,又BC⊆面SBC,根据面面垂直的判定定理平面SAB⊥平面SBC,
(Ⅱ)连接AC,由SA⊥平面ABCD,推断出AC是SC在底面ABCD内的射影,进而可知∠SCA为直线SC与底面ABCD所成角,求得A,又SA=2,进而求得tan∠SCA的值,即直线SC与底面ABCD所成角的正切值为
.
(Ⅱ)连接AC,由SA⊥平面ABCD,推断出AC是SC在底面ABCD内的射影,进而可知∠SCA为直线SC与底面ABCD所成角,求得A,又SA=2,进而求得tan∠SCA的值,即直线SC与底面ABCD所成角的正切值为
| ||
| 2 |
解答:
 (Ⅰ)证明:∵SA⊥平面ABCD,BC⊆平面ABCD
(Ⅰ)证明:∵SA⊥平面ABCD,BC⊆平面ABCD
∴SA⊥BC,
又∵∠ABC=90°即AB⊥BC
∵AB、SA⊆面SAB
∴BC⊥面SAB,
DSACB
又∵BC⊆面SBC
∴平面SAB⊥平面SBC,
(Ⅱ)解:连接AC
∵SA⊥平面ABCD
∴AC是SC在底面ABCD内的射影
∴∠SCA为直线SC与底面ABCD所成角,
∵AB=BC=2,∠ABC=90°
∴AC=2
又∵SA=2
∴tan∠SCA=
=
,即直线SC与底面ABCD所成角的正切值为
.
 (Ⅰ)证明:∵SA⊥平面ABCD,BC⊆平面ABCD
(Ⅰ)证明:∵SA⊥平面ABCD,BC⊆平面ABCD∴SA⊥BC,
又∵∠ABC=90°即AB⊥BC
∵AB、SA⊆面SAB
∴BC⊥面SAB,
DSACB
又∵BC⊆面SBC
∴平面SAB⊥平面SBC,
(Ⅱ)解:连接AC
∵SA⊥平面ABCD
∴AC是SC在底面ABCD内的射影
∴∠SCA为直线SC与底面ABCD所成角,
∵AB=BC=2,∠ABC=90°
∴AC=2
| 2 |
又∵SA=2
∴tan∠SCA=
| 2 | ||
2
|
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查了面面垂直的判定定理的应用,直线与平面所成的二面角.考查了学生基础知识综合运用.

练习册系列答案
相关题目
已知数列{an}满足a1=1,an+1=an+3,则a1+a2+a3+…+a10=( )
| A、130 | B、145 |
| C、160 | D、165 |
已知向量
、
的夹角为45°,且|
|=1,|2
-
|=
,则|
|=( )
| a |
| b |
| a |
| a |
| b |
| 10 |
| b |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |
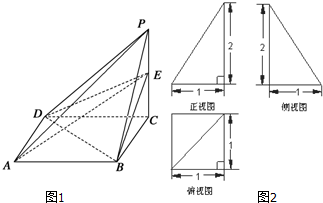
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.