Question

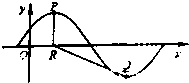已知函数f（x）=Asin（

π

3

x+φ），x∈R，A＞0，0＜φ＜

π

2

．y=f（x）的部分图象如图所示，P，Q分别为该图象的最高点和最低点，点P的坐标为（1，A）．若点R的坐标为（1，0），∠PRQ=

2π

3

，则A的值等于（　　）

• A、

  3

  3

• B、

  3

  2

• C、

  3

• D、2

  3

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：根据周期公式求出函数f（x）的最小正周期，由图象和条件设出点Q的坐标，再过点Q做x轴的垂线，设垂足为M，根据条件和正切函数求出A．

解答： 解：由题意得，函数f（x）的最小正周期T=

2π

π 3

=6，
由点P的坐标为（1，A），设点Q的坐标为（4，-A），
过点Q做x轴的垂线，设垂足为M，则RM=3，
∵∠PRQ=

2π

3

，∴∠MRQ=

2π

3

-

π

2

=

π

6

，
∴|MQ|=A=3×tan

π

6

=

3

，
故选：C．

点评：本题考查了y=Asin（ωx+φ）的周期和图象的关系，以及A的几何意义，构造直角三角形和求角是关键，考查识图能力，属于中档题．