题目内容
设某种产品分两道工序生产，第一道工序的次品率为10%，第二道工序的次品率为3%．生产这种产品只要有一道工序出次品就出次品，则该产品的次品率是（ ）
| A、0.13 | B、0.03 |
| C、0.127 | D、0.873 |
考点：相互独立事件的概率乘法公式
专题：计算题,概率与统计
分析：利用相互独立事件的概率乘法公式求得产品的正品率，利用对立事件的概率公式，可求产品的次品率．
解答：
解：由题意可得，当经过这第一道工序出来的产品是正品，且经过这第二道工序出来的产品也是正品时，得到的产品才是正品．
经过这每道工序出来的产品是否为正品，是相互独立的．第一道工序的正品率为1-10%，
第二道工序的正品率为1-3%，故产品的正品率为（1-10%）•（1-3%）=0.873，
所以产品的次品率是1-0.873=0.127．
故选：C．
经过这每道工序出来的产品是否为正品，是相互独立的．第一道工序的正品率为1-10%，
第二道工序的正品率为1-3%，故产品的正品率为（1-10%）•（1-3%）=0.873，
所以产品的次品率是1-0.873=0.127．
故选：C．
点评：本题主要考查相互独立事件的概率乘法公式的应用，考查对立事件的概率公式，属于中档题．
练习册系列答案
相关题目
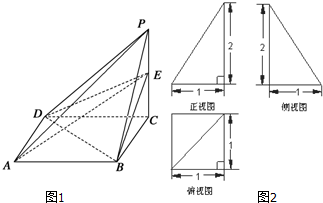
三棱椎的三视图为如图所示的三个直角三角形，则三棱锥的表面积为（ ）
A、4+4
| ||||
B、2+2
| ||||
C、
| ||||
D、2+2
|
已知
=（1，1，0），
=（-1，0，2），且k
+
与2
-
垂直，则k的值为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
| B、1 | ||
C、
| ||
D、
|
已知f（x）=
是R上的增函数，则a的取值范围是（ ）
|
| A、（0，1） |
| B、（1，4] |
| C、（1，+∞） |
| D、[4，+∞） |
已知数列{an}满足a1=1，an+1=an+3，则a1+a2+a3+…+a10=（ ）
| A、130 | B、145 |
| C、160 | D、165 |
已知向量
=（cos75°，sin75°），
=（cos15°，sin15°），那么|
+2
|的值为（ ）
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、3 |
已知向量
，
是夹角为60°的两个单位向量，向量
+λ
（λ∈R）与向量
-2
垂直，则实数λ的值为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、2 | D、0 |
