题目内容
设复数z满足z(2-3i)=6+4i(i为虚数单位),则z的模为 .
考点:复数求模
专题:数系的扩充和复数
分析:由条件利用两个复数商的模等于被除数的模除以除数的模,计算求得结果.
解答:
解:∵复数z满足z(2-3i)=6+4i(i为虚数单位),
∴z=
,∴|z|=
=
=2,
故答案为:2.
∴z=
| 6+4i |
| 2-3i |
| |6+4i| |
| |2-3i| |
| ||
|
故答案为:2.
点评:本题主要考查复数的模的定义,复数求模的方法,利用了两个复数商的模等于被除数的模除以除数的模,属于基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知函数f(x)=
,则函数y=f[f(x)]-1的零点个数为( )
|
| A、1 | B、2 | C、3 | D、4 |
已知数列{an}满足a1=1,an+1=an+3,则a1+a2+a3+…+a10=( )
| A、130 | B、145 |
| C、160 | D、165 |
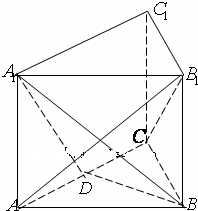 如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱垂直于底面,侧棱长为
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱垂直于底面,侧棱长为