题目内容
已知函数f(x)=lnx+
.
(1)当a=1时,求f(x)的极值;
(2)若f(x)在[2
上是单调递增的,求实数a的取值范围.(e为自然对数的底数)
| a |
| x |
(1)当a=1时,求f(x)的极值;
(2)若f(x)在[2
|
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)利用导数求函数的极值即可;
(2)由题意得f′(x)=
-
=
≥0在[2
上恒成立,即可得出结论.
(2)由题意得f′(x)=
| 1 |
| x |
| a |
| x2 |
| x-a |
| x2 |
|
解答:
解:(1)当a=1时,f(x)=lnx+
,
∴f′(x)=
-
=
=0,∴x=1,
∴当x>1时,f′(x)>0,f(x)在(1,+∞)上为增函数,
当0<x<1时,f′(x)<0,f(x)在(0,1)上为减函数,
∴当x=1时,函数有极小值为f(1)=1.
(2)f′(x)=
-
=
,
∵f(x)在[2
上是单调递增的,
∴f′(x)=
-
=
≥0在[2
上恒成立,
∴a≤2.
| 1 |
| x |
∴f′(x)=
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
∴当x>1时,f′(x)>0,f(x)在(1,+∞)上为增函数,
当0<x<1时,f′(x)<0,f(x)在(0,1)上为减函数,
∴当x=1时,函数有极小值为f(1)=1.
(2)f′(x)=
| 1 |
| x |
| a |
| x2 |
| x-a |
| x2 |
∵f(x)在[2
|
∴f′(x)=
| 1 |
| x |
| a |
| x2 |
| x-a |
| x2 |
|
∴a≤2.
点评:本题主要考查利用导数研究函数的单调性,求函数的极值等知识,属于基础题,应熟练掌握.

练习册系列答案
相关题目
下列命题中为真命题的是( )
| A、?x∈R,x2+2x+1=0 | ||
B、?x0∈R,-
| ||
| C、?x∈N*,log2x>0 | ||
| D、?x0∈R,cos x0>x02+2x0+3 |
函数f(x)=
的定义域为M,g(x)=
的定义域为N,则M∩N=( )
| 1 | ||
|
| x+2 |
| A、[-2,+∞) |
| B、[-2,2) |
| C、(-2,2) |
| D、(-∞,2) |
设S是至少含有两个元素的集合,在S上定义了一个运算“※”(即对任意的a、b∈S,对于有序元素对(a,b),在S中有唯一确定的元素a※b与之对应),若对任意的a、b∈S,有a※(b※a)=b,下列等式中不恒成立的是( )
| A、(a※b)※a=a |
| B、[a※(b※a)]※(a※b)=a |
| C、b※(b※b)=b |
| D、(a※b)※[b※(a※b)]=b |
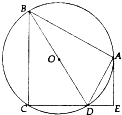 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.