Question

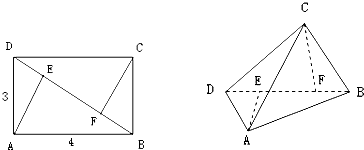如图，已知矩形ABCD中，AB=2，AD=1，AE⊥BD，CF⊥BD，沿对角线BD把△BCD折起，使二面角C-BD-A的大小为60°，则线段AC的长为

 

．

Answer 1

考点：二面角的平面角及求法

专题：计算题,空间位置关系与距离,空间角

分析：首先在矩形ABCD中，分别求出AE，EF，CF的长，在平面ABD内，过F作FH∥AE，且FH=AE，连接AH，易得四边形AEFH为矩形，由FH⊥DB，又CF⊥DB，即有∠CFH为二面角C-BD-A的平面角，且为60°，求得CH，再由线面垂直得到△ACH为直角三角形，由勾股定理，即可得到AC的长．

解答： 解：在直角三角形ABD中，AB=2，AD=1，BD=

5

，
AE=

2

5

，DE=

1- 4 5

=

1

5

，
同理直角三角形ABC中，CF=

2

5

，BF=

1

5

，
则EF=BD-DE-BF=

3

5

，
在平面ABD内，过F作FH∥AE，且FH=AE，连接AH，易得四边形AEFH为矩形，
则AH=EF=

3

5

，AH∥EF，
FH⊥DB，又CF⊥DB，即有∠CFH为二面角C-BD-A的平面角，且为60°，
即CH=CF=

2

5

，
由BD⊥平面CFH，得到BD⊥CH，
即有AH⊥CH，
则AC=

AH2+CH2

=

9 5 + 4 5

=

65

5

．
故答案为：

65

5

．

点评：本题主要考查空间的二面角的求法，考查空间线面的位置关系，同时考查基本的运算能力，属于中档题．