题目内容
设集合A={x|x＜
}，a=2
，那么下列关系正确的是（ ）
| 21 |
| 3 |
| A、a⊆A | B、{a}∈A |
| C、a∉A | D、a∈A |
考点：元素与集合关系的判断
专题：计算题
分析：利用平方法比较2
与
的大小，可得a为集合A的元素，由此可得答案．
| 3 |
| 21 |
解答：
解：∵a=2
＜
，∴a为集合A的元素，
∴a∈A．
故选：D．
| 3 |
| 21 |
∴a∈A．
故选：D．
点评：本题考查了元素与集合之间的关系，利用平方法比较2
与
的大小是关键．
| 3 |
| 21 |
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
设f（x）=ax2+（b-8）x-a-ab，若不等式f（x）＜0的解集是（-∞，-3）∪（2，+∞），则a+b=（ ）
| A、-8 | B、-2 | C、8 | D、2 |
为了稳定市场，确保农民增收，某农产品3月以后的每月市场收购价格与其前三个月的市场收购价格有关，并使其与前三个月的市场收购价格之差的平方和最小，下表列出的是该产品今年前六个月的市场收购价格，则前七个月该产品的市场收购价格的方差为（ ）
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 价格（元/担） | 68 | 78 | 67 | 71 | 72 | 70 |
A、
| ||
B、
| ||
| C、11 | ||
D、
|
若复数z=i+i2014，则复数
+
（i为虚数单位）在复平面内对应的点所在象限为（ ）
. |
| z |
| 10 |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知方程
+
=1表示椭圆，则k的取值范围（ ）
| x2 |
| 3+k |
| y2 |
| 2+k |
| A、k＞-3 | B、-3＜k＜-2 |
| C、k＞-2 | D、k＜-3 |
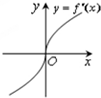已知定义在R上的函数f（x）满足f（-1）=f（3）=1，f′（x）为f（x）的导函数，且导函数y=f′（x）的图象如图所示．则不等式f（x）＜1的解集是（ ）| A、（-1，0） |
| B、（-1，3） |
| C、（0，3） |
| D、（-∞，-1）（3，+∞） |