题目内容
某校一天要上语文、数学、外语、历史、政治、体育六节课,在所有可能的安排中,数学不排在最后一节,体育不排在第一节的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:本题考查古典概型中利用排列组合求基本事件个数,再求概率的类型,有2个特殊元素,从其中一个数学开始讨论,分2种情况讨论即可.
解答:
解:从元素入手,特殊元素优先,先排数学,分2类:
①当数学在第一节时,其他5个元素全排列
即可,
②当数学不在第一节时,也不排在最后一节,则应为
;再排体育,又不排在第一节,应为
,然后剩下4个元素全排列
,即本类排法为
,
综上共有
+
=504
又基本事件共有
=720
所以概率P=
=
,
故答案为:
.
①当数学在第一节时,其他5个元素全排列
| A | 5 5 |
②当数学不在第一节时,也不排在最后一节,则应为
| A | 1 4 |
| A | 1 4 |
| A | 4 4 |
| A | 1 4 |
| A | 1 4 |
| A | 4 4 |
综上共有
| A | 5 5 |
| A | 1 4 |
| A | 1 4 |
| A | 4 4 |
又基本事件共有
| A | 6 6 |
所以概率P=
| 504 |
| 720 |
| 7 |
| 10 |
故答案为:
| 7 |
| 10 |
点评:利用排列组合求概率,属于排列中的特殊元素特殊位置类型,从元素入手或者从位置入手都可,但讨论标准讨论完前,不可更换.

练习册系列答案
相关题目
设集合A={x|x<
},a=2
,那么下列关系正确的是( )
| 21 |
| 3 |
| A、a⊆A | B、{a}∈A |
| C、a∉A | D、a∈A |
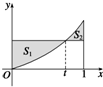 在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积:
在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积: