题目内容
已知复数z1=cosx+i,z2=1-isinx,x∈R.
(1)求|z1-z2|的最小值;
(2)设z=z1•z2,记f(x)=Imz(Imz表示复数z的虚部).将函数f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得的图象向右平移
个单位长度,得到函数g(x)的图象.试求函数g(x)的解析式.
(1)求|z1-z2|的最小值;
(2)设z=z1•z2,记f(x)=Imz(Imz表示复数z的虚部).将函数f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得的图象向右平移
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,复数代数形式的混合运算
专题:三角函数的图像与性质
分析:(1)利用已知条件直接求解|z1-z2|,得到表达式后,利用三角函数的最值求解复数的模的最小值;
(2)化简z=z1•z2,求出函数f(x)的表达式,利用图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得的图象向右平移
个单位长度,求出函数g(x)的图象对应的函数g(x)的解析式.
(2)化简z=z1•z2,求出函数f(x)的表达式,利用图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得的图象向右平移
| π |
| 2 |
解答:
解(1)∵复数z1=cosx+i,z2=1-isinx,x∈R,
∴|z1-z2|=
=
.
∴当sin(x-
)=-1,即x=2kπ-
,k∈Z时,
|z1-z2|min=
=
-1.
(2)∵z=z1•z2,
∴z=z1•z2=sinx+cosx+(1-sinxcosx)i.
f(x)=Imz(Imz表示复数z的虚部).
∴f(x)=1-sinxcosx=1-
sin2x,x∈R..
将函数f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后,
得到的图象所对应的函数是y1=1-
sinx.
把函数y=1-
sinx的图象向右平移
个单位长度,得到的图象对应的函数是y=1-
sin(x-
).
∴g(x)=1-
sin(x-
)=1+
cosx,x∈R.
∴|z1-z2|=
| (cosx-1)2+(1+sinx)2 |
3+2
|
∴当sin(x-
| π |
| 4 |
| π |
| 4 |
|z1-z2|min=
3-2
|
| 2 |
(2)∵z=z1•z2,
∴z=z1•z2=sinx+cosx+(1-sinxcosx)i.
f(x)=Imz(Imz表示复数z的虚部).
∴f(x)=1-sinxcosx=1-
| 1 |
| 2 |
将函数f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后,
得到的图象所对应的函数是y1=1-
| 1 |
| 2 |
把函数y=1-
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
∴g(x)=1-
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
点评:本题以复数为载体,考查三角函数的化简求值,函数的图象的变换,基本知识的考查.

练习册系列答案
相关题目
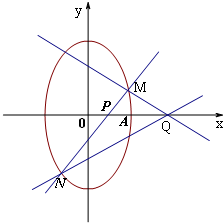 已知椭圆C:
已知椭圆C: