题目内容
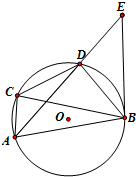如图，已知四边形ABCD内接于圆O，过B作圆O的切线交AD的延长线于E，若BD是∠CBE的平分线．证明：（Ⅰ）AD是∠BAC的平分线；
（Ⅱ）AB•BE=AE•CD．
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：（Ⅰ）证明AD是∠BAC的平分线，只需证明∠CAD=∠BAD，利用BE是圆O的切线，BD是∠CBE的平分线即可证明；
（Ⅱ）由（Ⅰ）知，△ABE∽△BDE，可得
=
，证明BD=CD，即可证明AB•BE=AE•CD．
（Ⅱ）由（Ⅰ）知，△ABE∽△BDE，可得
| AE |
| BE |
| AB |
| BD |
解答：
证明：（Ⅰ）∵BE是圆O的切线，
∴∠EBD=∠BAD=∠BCD，
∵BD是∠CBE的平分线，
∴∠CBD=∠BAD，
∴∠CAD=∠CBD=∠BAD，
∴AD是∠BAC的平分线；
（Ⅱ）由（Ⅰ）知，△ABE∽△BDE，
∴
=
，
在△BCD中，∠BCD=∠CBD，
∴BD=CD，
∴
=
，
∴AB•BE=AE•CD．
∴∠EBD=∠BAD=∠BCD，
∵BD是∠CBE的平分线，
∴∠CBD=∠BAD，
∴∠CAD=∠CBD=∠BAD，
∴AD是∠BAC的平分线；
（Ⅱ）由（Ⅰ）知，△ABE∽△BDE，
∴
| AE |
| BE |
| AB |
| BD |
在△BCD中，∠BCD=∠CBD，
∴BD=CD，
∴
| AE |
| BE |
| AB |
| CD |
∴AB•BE=AE•CD．
点评：本题考查与圆有关的比例线段，考查三角形相似的判断与运用，难度中等．
练习册系列答案
习题精选系列答案
相关题目
已知等比数列{an}的各项都为正数，且以a1+a2＞2a3，则公比q的取值范围是（ ）
A、（0，
| ||
B、（
| ||
| C、（0，1） | ||
| D、（1，+∞） |
如图，△ABC内接于圆O，∠A的平分线交BC于点D，交外接圆于点E，求证：AD2=AB•AC-BD•DC．