题目内容
已知函数f(x)=ln
,g(x)=
,a>0.
(1)若曲线y=f(x)在(1,f(1))处的切线方程为x-y-1=0,求a的值;
(2)证明:当x>a时,f(x)的图象始终在g(x)的图象的下方;
(3)当a=1时,设曲线C:h(x)=f(x)-e[1+
•g(x)](e为自然对数的底数),h′(x)表示h(x)的导函数,求证:对于曲线C上的不同两点A(x1,y1),B(x2,y2),x1<x2,存在唯一的x0∈(x1,x2),使直线AB的斜率等于h′(x0).
| x |
| a |
| x-a | ||
|
(1)若曲线y=f(x)在(1,f(1))处的切线方程为x-y-1=0,求a的值;
(2)证明:当x>a时,f(x)的图象始终在g(x)的图象的下方;
(3)当a=1时,设曲线C:h(x)=f(x)-e[1+
| x |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:(1)已知曲线上的点,并且知道过此点的切线方程,容易求出斜率,又知点(1,f(1))在曲线上,利用方程联立解出a的值;
(2)令φ(x)=f(x)-g(x)=lnx-lna-
(x>a>0),证明φ(x)在(a,+∞)上单调递减,且φ(a)=0,即可得出结论;
(3)若存在唯一的x0∈(x1,x2),使直线AB的斜率等于h′(x0),则x0ln
-(x2-x1)=0,设F(x)=xln
-(x2-x1),则F(x)是关于x的一次函数,只需证明F(x)在(x1,x2)上单调,且满足F(x1)F(x2)<0.将x1,x2看作自变量,得到两个新函数足F(x1)、F(x2),讨论它们的最值即可.
(2)令φ(x)=f(x)-g(x)=lnx-lna-
| x-a | ||
|
(3)若存在唯一的x0∈(x1,x2),使直线AB的斜率等于h′(x0),则x0ln
| x2 |
| x1 |
| x2 |
| x1 |
解答:
(1)解:∵f(x)=ln
,
∴f′(x)=
,
∴f′(1)=1,
∵f(1)=ln
,
∵曲线y=f(x)在(1,f(1))处的切线方程为x-y-1=0,
∴1-ln
-1=0,
∴a=1;
(2)解:令φ(x)=f(x)-g(x)=lnx-lna-
(x>a>0),则φ′(x)=-
<0,
∴φ(x)在(a,+∞)上单调递减,且φ(a)=0,
∴x>a时,φ(x)<φ(a)=0,即f(x)<g(x),
∴当x>a时,f(x)的图象始终在g(x)的图象的下方;
(3)证明:由题意,h(x)=lnx-ex,
若存在唯一的x0∈(x1,x2),使直线AB的斜率等于h′(x0),
则
-e=
,
∴x0ln
-(x2-x1)=0,
设F(x)=xln
-(x2-x1),则F(x)是关于x的一次函数,
∴只需证明F(x)在(x1,x2)上单调,且满足F(x1)F(x2)<0.
F(x1)=x1ln
-(x2-x1),F(x2)=x2ln
-(x2-x1),
将x1,x2看作自变量,得到两个新函数足F(x1)、F(x2),讨论它们的最值.
F(x1)=x1ln
-(x2-x1),F′(x1)=ln
>0,函数是增函数,
∵x1<x2,
∴F(x1)<F(x2)=0.
同理F(x2)=x2ln
-(x2-x1),函数是增函数,∴F(x1)>F(x2)=0.
∴F(x1)F(x2)<0
∴F(x)=xln
-(x2-x1)在(x1,x2)上有零点x0,
∵
>1,
∴ln
>0,
∴F(x)=xln
-(x2-x1),)在(x1,x2)上是增函数,
∴F(x)=xln
-(x2-x1)在(x1,x2)上有唯一零点x0,
∴对于曲线C上的不同两点A(x1,y1),B(x2,y2),x1<x2,存在唯一的x0∈(x1,x2),使直线AB的斜率等于h′(x0).
| x |
| a |
∴f′(x)=
| 1 |
| x |
∴f′(1)=1,
∵f(1)=ln
| 1 |
| a |
∵曲线y=f(x)在(1,f(1))处的切线方程为x-y-1=0,
∴1-ln
| 1 |
| a |
∴a=1;
(2)解:令φ(x)=f(x)-g(x)=lnx-lna-
| x-a | ||
|
(
| ||||
2x
|
∴φ(x)在(a,+∞)上单调递减,且φ(a)=0,
∴x>a时,φ(x)<φ(a)=0,即f(x)<g(x),
∴当x>a时,f(x)的图象始终在g(x)的图象的下方;
(3)证明:由题意,h(x)=lnx-ex,
若存在唯一的x0∈(x1,x2),使直线AB的斜率等于h′(x0),
则
| 1 |
| x0 |
| lnx2-lnx1-e(x2-x1) |
| x2-x1 |
∴x0ln
| x2 |
| x1 |
设F(x)=xln
| x2 |
| x1 |
∴只需证明F(x)在(x1,x2)上单调,且满足F(x1)F(x2)<0.
F(x1)=x1ln
| x2 |
| x1 |
| x2 |
| x1 |
将x1,x2看作自变量,得到两个新函数足F(x1)、F(x2),讨论它们的最值.
F(x1)=x1ln
| x2 |
| x1 |
| x2 |
| x1 |
∵x1<x2,
∴F(x1)<F(x2)=0.
同理F(x2)=x2ln
| x2 |
| x1 |
∴F(x1)F(x2)<0
∴F(x)=xln
| x2 |
| x1 |
∵
| x2 |
| x1 |
∴ln
| x2 |
| x1 |
∴F(x)=xln
| x2 |
| x1 |
∴F(x)=xln
| x2 |
| x1 |
∴对于曲线C上的不同两点A(x1,y1),B(x2,y2),x1<x2,存在唯一的x0∈(x1,x2),使直线AB的斜率等于h′(x0).
点评:本题考查导数知识的综合运用,考查导数的几何意义,考查学生分析解决问题的能力,正确构造函数是关键.

练习册系列答案
相关题目
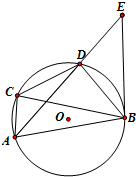 如图,已知四边形ABCD内接于圆O,过B作圆O的切线交AD的延长线于E,若BD是∠CBE的平分线.证明:
如图,已知四边形ABCD内接于圆O,过B作圆O的切线交AD的延长线于E,若BD是∠CBE的平分线.证明: 如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧