题目内容
 如图,△ABC内接于圆O,∠A的平分线交BC于点D,交外接圆于点E,求证:AD2=AB•AC-BD•DC.
如图,△ABC内接于圆O,∠A的平分线交BC于点D,交外接圆于点E,求证:AD2=AB•AC-BD•DC.考点:与圆有关的比例线段
专题:选作题,立体几何
分析:连接EC,证出∠BAE=∠CAE,∠ABC=∠AEC,得出△ABD∽△AEC,可得AB•AC=AD•AE,再利用相交弦定理,即可得出结论..
解答:
解:连接EC,
∵EA是∠BAC的平分线,
∴∠BAE=∠CAE,
∵∠ABC=∠AEC,
∴△ABD∽△AEC,
∴
=
,
∴AB•AC=AD•AE.
∵BD•DC=AD•DE,
∴两式相减可得AD2=AB•AC-BD•DC.

∵EA是∠BAC的平分线,
∴∠BAE=∠CAE,
∵∠ABC=∠AEC,
∴△ABD∽△AEC,
∴
| AB |
| AE |
| AD |
| AC |
∴AB•AC=AD•AE.
∵BD•DC=AD•DE,
∴两式相减可得AD2=AB•AC-BD•DC.
点评:此题考查了圆周角定理,关键是根据圆周角定理和已知条件证出△ABD∽△AEC,用到的知识点是圆周角定理、相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
i是虚数单位,复数(
)2表示的点落在哪个象限( )
| 3-i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知n∈N,常数p,q均大于1,且都不等于2,则
=( )
| lim |
| n→∞ |
| pn+1-qn |
| pn+2-2qn+1 |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
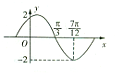 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤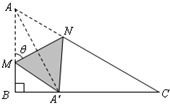 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC=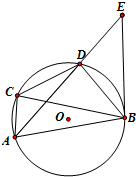 如图,已知四边形ABCD内接于圆O,过B作圆O的切线交AD的延长线于E,若BD是∠CBE的平分线.证明:
如图,已知四边形ABCD内接于圆O,过B作圆O的切线交AD的延长线于E,若BD是∠CBE的平分线.证明: