题目内容
已知等比数列{an}的各项都为正数,且以a1+a2>2a3,则公比q的取值范围是( )
A、(0,
| ||
B、(
| ||
| C、(0,1) | ||
| D、(1,+∞) |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:利用等比数列的通项公式,结合等比数列{an}的各项都为正数,解不等式,即可求出公比q的取值范围.
解答:
解:∵a1+a2>2a3,
∴a1+a1q>2a1q2,
∵等比数列{an}的各项都为正数,
∴2q2-q-1<0,q>0,
∴0<q<1.
故选:C.
∴a1+a1q>2a1q2,
∵等比数列{an}的各项都为正数,
∴2q2-q-1<0,q>0,
∴0<q<1.
故选:C.
点评:本题考查等比数列的通项公式,考查学生的计算能力,属于基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
设命题p:?x0>0,使x02+2x0+a=0(a为实常数),则¬p为假命题的一个充分不必要条件是( )
| A、a<0 | B、a≤-1 |
| C、a<l | D、a>-2 |
阅读程序框图,若输出的函数值在区间[0,4]上,则输入的实数x的取值范围是( )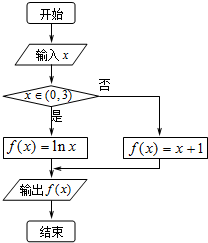

| A、{x∈R|-1≤x≤0或1≤x≤3} |
| B、{x∈R|-1≤x≤0或1≤x<3} |
| C、{x∈R|-1≤x≤0或1≤x≤e4} |
| D、{x∈R|-1≤x≤3} |
能够把圆O:x2+y2=r2(r>0)的周长和面积同时分为相等的两部分的函数称之为圆O的“和谐函数”,下列函数不是圆O的“和谐函数”的是( )
| A、f(x)=4x3+x | ||
B、f(x)=ln
| ||
C、f(x)=tan
| ||
| D、f(x)=ex+e-x |
 三棱锥P-ABC的三视图如图所示,其中P是直角顶点.设M是面ABC内一点.定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(6,x,y),且
三棱锥P-ABC的三视图如图所示,其中P是直角顶点.设M是面ABC内一点.定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(6,x,y),且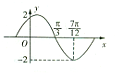 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤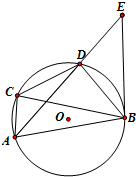 如图,已知四边形ABCD内接于圆O,过B作圆O的切线交AD的延长线于E,若BD是∠CBE的平分线.证明:
如图,已知四边形ABCD内接于圆O,过B作圆O的切线交AD的延长线于E,若BD是∠CBE的平分线.证明: