题目内容
已知函数f(x)=x2-ax+ln
(a>0).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若对任意a∈(1,2),总存在x0∈[
,1],使不等式f(x0)>k(1-a2)成立,求实数k的取值范围.
| ax+1 |
| 2 |
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若对任意a∈(1,2),总存在x0∈[
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,分类讨论,利用导数的正负,即可求得函数f(x)的单调性;
(Ⅱ)a∈(1,2)时,f(x)在[
,1]上的最大值为f(1)=ln(
+
a)+1-a,于是问题等价于:对任意的a∈(1,2),不等式ln(
+
a)+1-a+k(a2-1)>0恒成立,再利用导函数研究不等式左边的最小值看是否符合要求即可求实数m的取值范围.
(Ⅱ)a∈(1,2)时,f(x)在[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)由题得:f′(x)=
∴a>
时,由f′(x)>0可得单调增区间为(-∞,0),(
,+∞),由f′(x)<0可得单调减区间为(0,
),
0<a<
时,由f′(x)>0可得单调增区间为(-∞,
),(0,+∞),由f′(x)<0可得单调减区间为(
,0),
a=
时,f′(x)≥0,单调增区间为R;
(Ⅱ)a∈(1,2)时,f(x)在[
,1]上的最大值为f(1)=ln(
+
a)+1-a,
于是问题等价于:对任意的a∈(1,2),不等式ln(
+
a)+1-a+k(a2-1)>0恒成立.
记g(a)=ln(
+
a)+1-a+k(a2-1),(1<a<2)
则g′(a)=
[2ka-(1-2k)],
当k=0时,g′(a)=
<0,
∴g(a)在区间(1,2)上递减,此时,g(a)<g(1)=0,
由于a2-1>0,
∴k≤0时不可能使g(a)>0恒成立,
故必有k>0,∴g′(a)=
[2ka-(1-2k)].
若
-1>1,可知g(a)在区间(1,min{2,
-1})上递减,在此区间上,有g(a)<g(1)=0,与g(a)>0恒成立矛盾,故
-1≤1,
这时,g'(a)>0,g(a)在(1,2)上递增,恒有g(a)>g(1)=0,满足题设要求,
∴
,即k≥
,
∴实数k的取值范围为[
,+∞).
2ax(x-
| ||
| ax+1 |
∴a>
| 2 |
| a2-2 |
| 2a |
| a2-2 |
| 2a |
0<a<
| 2 |
| a2-2 |
| 2a |
| a2-2 |
| 2a |
a=
| 2 |
(Ⅱ)a∈(1,2)时,f(x)在[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
于是问题等价于:对任意的a∈(1,2),不等式ln(
| 1 |
| 2 |
| 1 |
| 2 |
记g(a)=ln(
| 1 |
| 2 |
| 1 |
| 2 |
则g′(a)=
| a |
| 1+a |
当k=0时,g′(a)=
| -a |
| 1+a |
∴g(a)在区间(1,2)上递减,此时,g(a)<g(1)=0,
由于a2-1>0,
∴k≤0时不可能使g(a)>0恒成立,
故必有k>0,∴g′(a)=
| a |
| 1+a |
若
| 1 |
| 2k |
| 1 |
| 2k |
| 1 |
| 2k |
这时,g'(a)>0,g(a)在(1,2)上递增,恒有g(a)>g(1)=0,满足题设要求,
∴
|
| 1 |
| 4 |
∴实数k的取值范围为[
| 1 |
| 4 |
点评:本题考查利用导数研究函数单调性,考查函数恒成立问题,考查函数与方程思想、分类讨论思想,综合性强,难度大.

练习册系列答案
相关题目
能够把圆O:x2+y2=r2(r>0)的周长和面积同时分为相等的两部分的函数称之为圆O的“和谐函数”,下列函数不是圆O的“和谐函数”的是( )
| A、f(x)=4x3+x | ||
B、f(x)=ln
| ||
C、f(x)=tan
| ||
| D、f(x)=ex+e-x |
已知n∈N,常数p,q均大于1,且都不等于2,则
=( )
| lim |
| n→∞ |
| pn+1-qn |
| pn+2-2qn+1 |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
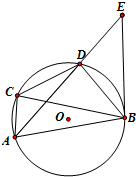 如图,已知四边形ABCD内接于圆O,过B作圆O的切线交AD的延长线于E,若BD是∠CBE的平分线.证明:
如图,已知四边形ABCD内接于圆O,过B作圆O的切线交AD的延长线于E,若BD是∠CBE的平分线.证明: 如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧