题目内容
已知关于x的方程lnx=mx,x∈(0,a),若存在a,m,使此方程有两个不同的实数解,则称实数对(a,m)为此方程的“D-S-P”,则在(
,-
),(
,
),(2e,
),(e2,
)中,“D-S-P”点有( )
| 1 |
| 2 |
| 1 |
| e |
| e |
| 1 | ||
3
|
| 2ln2 |
| e |
| 5 |
| 2e2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:利用导数研究曲线上某点切线方程
专题:综合题,函数的性质及应用
分析:当l与C相切时,利用导数求得切点横坐标为x0=e,切线斜率为m=
,只要a>e,
<m<
即可(
=
为(a,lna)与原点连线的斜率).
| 1 |
| e |
| lna |
| a |
| 1 |
| e |
| lna |
| a |
| lna-0 |
| a-0 |
解答:
 解:由题意,如图所示,
解:由题意,如图所示,
当l与C相切时,利用导数求得切点横坐标为x0=e,切线斜率为m=
,
∴只要a>e,
<m<
即可(
=
为(a,lna)与原点连线的斜率).
对于(
,-
),∵-
<0,∴(
,-
)不是“D-S-P”点;
对于(
,
),∵
<e,∴(
,
)不是“D-S-P”点;
对于(2e,
),∵
>
,∴(2e,
)不是“D-S-P”点;
对于(e2,
),∵e2>e,
=
=
<
<
,∴(e2,
)是“D-S-P”点.
故选:A.
 解:由题意,如图所示,
解:由题意,如图所示,当l与C相切时,利用导数求得切点横坐标为x0=e,切线斜率为m=
| 1 |
| e |
∴只要a>e,
| lna |
| a |
| 1 |
| e |
| lna |
| a |
| lna-0 |
| a-0 |
对于(
| 1 |
| 2 |
| 1 |
| e |
| 1 |
| e |
| 1 |
| 2 |
| 1 |
| e |
对于(
| e |
| 1 | ||
3
|
| e |
| e |
| 1 | ||
3
|
对于(2e,
| 2ln2 |
| e |
| 2ln2 |
| e |
| 1 |
| e |
| 2ln2 |
| e |
对于(e2,
| 5 |
| 2e2 |
| lna |
| a |
| 2 |
| e2 |
| 4 |
| 2e2 |
| 5 |
| 2e2 |
| 1 |
| e |
| 5 |
| 2e2 |
故选:A.
点评:本题考查利用导数研究函数的性质、含参数的存在性问题,考查新定义,考查数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
能够把圆O:x2+y2=r2(r>0)的周长和面积同时分为相等的两部分的函数称之为圆O的“和谐函数”,下列函数不是圆O的“和谐函数”的是( )
| A、f(x)=4x3+x | ||
B、f(x)=ln
| ||
C、f(x)=tan
| ||
| D、f(x)=ex+e-x |
已知A(1,0),点B在曲线G:y=ln(x+1)上,若线段AB与曲线M:y=
相交且交点恰为线段AB的中点,则称B为曲线G关于曲线M的一个关联点.记曲线G关于曲线M的关联点的个数为a,则( )
| 1 |
| x |
| A、a=0 | B、a=1 |
| C、a=2 | D、a>2 |
i是虚数单位,复数(
)2表示的点落在哪个象限( )
| 3-i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设函数f(x)=3sin(2x+
)+1,将y=f(x)的图象向右平移φ(φ>0)个单位,使得到的图象关于y轴对称,则φ的最小值为( )
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知n∈N,常数p,q均大于1,且都不等于2,则
=( )
| lim |
| n→∞ |
| pn+1-qn |
| pn+2-2qn+1 |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
 三棱锥P-ABC的三视图如图所示,其中P是直角顶点.设M是面ABC内一点.定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(6,x,y),且
三棱锥P-ABC的三视图如图所示,其中P是直角顶点.设M是面ABC内一点.定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(6,x,y),且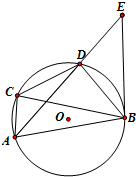 如图,已知四边形ABCD内接于圆O,过B作圆O的切线交AD的延长线于E,若BD是∠CBE的平分线.证明:
如图,已知四边形ABCD内接于圆O,过B作圆O的切线交AD的延长线于E,若BD是∠CBE的平分线.证明: