题目内容
已知函数f（x）=x2-5x+m的两个不等零点均大于1，求m的取值范围．
考点：一元二次方程的根的分布与系数的关系
专题：函数的性质及应用
分析：根据函数f（x）=x2-5x+m的两个不等零点均大于1，可得
，解此不等式组求得m的范围．
|
解答：
解：函数f（x）=x2-5x+m的两个不等零点均大于1，∴
．
解得 4＜m＜
，即m的取值范围是（4，
）．
|
解得 4＜m＜
| 25 |
| 4 |
| 25 |
| 4 |
点评：本题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，体现了转化的数学思想，属于中档题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
设命题p：?x0＞0，使x02+2x0+a=0（a为实常数），则￢p为假命题的一个充分不必要条件是（ ）
| A、a＜0 | B、a≤-1 |
| C、a＜l | D、a＞-2 |
已知A（1，0），点B在曲线G：y=ln（x+1）上，若线段AB与曲线M：y=
相交且交点恰为线段AB的中点，则称B为曲线G关于曲线M的一个关联点．记曲线G关于曲线M的关联点的个数为a，则（ ）
| 1 |
| x |
| A、a=0 | B、a=1 |
| C、a=2 | D、a＞2 |
设函数f（x）=3sin（2x+
）+1，将y=f（x）的图象向右平移φ（φ＞0）个单位，使得到的图象关于y轴对称，则φ的最小值为（ ）
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知n∈N，常数p，q均大于1，且都不等于2，则
=（ ）
| lim |
| n→∞ |
| pn+1-qn |
| pn+2-2qn+1 |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
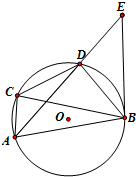如图，已知四边形ABCD内接于圆O，过B作圆O的切线交AD的延长线于E，若BD是∠CBE的平分线．证明：
如图，在直角梯形ABCD中，AB=AD=2，把此梯形绕其直角边AD旋转120°得到如图所示的几何体，点G是∠BDF平分线上任意一点（异于点D），点M是弧