题目内容
1．某多面体的三视图如图所示，则该多面体各面的面积中最大的是（ ）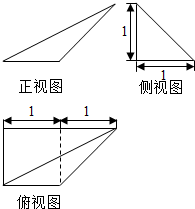
| A． | 1 | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\sqrt{5}$ |
分析 作出几何体的直观图，根据几何体的结构特征计算各个面的面积．
解答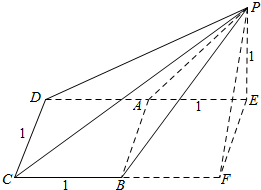 
解：由三视图可知该几何体为底面为正方形的四棱锥P-ABCD，P在底面的投影E在DA的延长线上，且PE=AE=AD=CD=1，
∴S△PAD=$\frac{1}{2}×AD×PE$=$\frac{1}{2}$，S底面ABCD=1×1=1，PA=$\sqrt{P{E}^{2}+A{E}^{2}}$=$\sqrt{2}$，PD=$\sqrt{P{E}^{2}+D{E}^{2}}$=$\sqrt{5}$，PF=$\sqrt{P{E}^{2}+E{F}^{2}}$=$\sqrt{2}$，
∴S△PCD=$\frac{1}{2}×CD×PD$=$\frac{\sqrt{5}}{2}$，S△PAB=$\frac{1}{2}×AB×PA$=$\frac{\sqrt{2}}{2}$．S△PBC=$\frac{1}{2}×BC×PF$=$\frac{\sqrt{2}}{2}$．
∴在四棱锥的五个面中，△PCD的面积最大．
故选C．
点评 本题考查了棱锥的结构特征和三视图，作出棱锥的直观图是解题关键．
练习册系列答案
相关题目
如图所示，在四棱锥P-ABCD中，四边形ABCD是边长为2的正方形，平面ABCD⊥平面PCD，∠PCD=90°，PC=1.5，E是侧棱PC上的动点．
6．
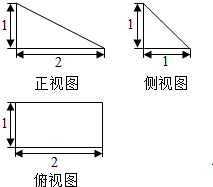某几何体的正视图、侧（左）视图、俯视图如图所示，若该几何体各个顶点在同一个球面上，则该球体的表面积是（ ）
某几何体的正视图、侧（左）视图、俯视图如图所示，若该几何体各个顶点在同一个球面上，则该球体的表面积是（ ）| A． | 6π | B． | 12π | C． | 24π | D． | 32π |
13．若A点坐标为（1，1），F1是椭圆5x2+9y2=45的左焦点，点P是该椭圆上的动点，则|PA|+|PF1|的最大值为（ ）
| A． | $6-\sqrt{2}$ | B． | $6+\sqrt{2}$ | C． | $5+\sqrt{2}$ | D． | $7+\sqrt{2}$ |
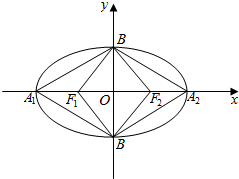如图所示，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），A1、A2、B1、B2、F1、F2分别是其左右顶点，上下顶点和左右焦点，四边形A1B1A2B2的面积是四边形B1F2B2F1面积的2倍．