题目内容
16.已知P为椭圆$\frac{x^2}{8}$+$\frac{y^2}{2}$=1上一个动点,A(-2,1),B(2,-1),设直线AP和BP分别与直线x=4交于M、N两点,若△ABP与△MNP的面积相等,则|OP|的值为$\frac{\sqrt{107}}{4}$.分析 设P(m,n),N(4,t),M(4,s),设m,n>0,代入椭圆方程,运用点到直线的距离,再由三点共线的条件:斜率相等,运用三角形的面积公式,化简整理,解方程可得m,n,再由两点的距离公式,计算即可得到所求值.
解答 解:设P(m,n),N(4,t),M(4,s),设m,n>0,
即有$\frac{{m}^{2}}{8}$+$\frac{{n}^{2}}{2}$=1,①
直线AB的方程为y=-$\frac{1}{2}$x,
P到AB的距离为d=$\frac{|m+2n|}{\sqrt{5}}$,
△PAB的面积为S=$\frac{1}{2}$•2$\sqrt{5}$•$\frac{|m+2n|}{\sqrt{5}}$=|m+2n|,
由A,M,P共线,可得$\frac{s+1}{2}$=$\frac{n+1}{m-2}$,
即有s=$\frac{2n-m+4}{m-2}$,
由B,N,P共线,可得$\frac{t-1}{6}$=$\frac{n-1}{m+2}$,
即有t=$\frac{m+6n-4}{m+2}$,
即有|s-t|=|$\frac{(m+2n)(8-2m)}{{m}^{2}-4}$|,
则△PMN的面积为$\frac{1}{2}$(4-m)•|$\frac{(m+2n)(8-2m)}{{m}^{2}-4}$|,
由△ABP与△MNP的面积相等,
可得(4-m)2=m2-4,②
解得m=$\frac{5}{2}$,n2=$\frac{14}{32}$,
则|OP|=$\sqrt{\frac{25}{4}+\frac{14}{32}}$=$\frac{\sqrt{107}}{4}$.
故答案为:$\frac{\sqrt{107}}{4}$.
点评 本题考查椭圆的方程的运用,考查三点共线的条件:斜率相等,考查三角形的面积公式的运用,以及化简整理的运算能力,属于中档题.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案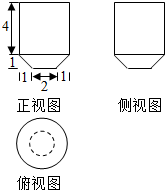
| A. | $\frac{53}{3}$π | B. | $\frac{55}{3}$π | C. | 18π | D. | $\frac{76}{3}$π |
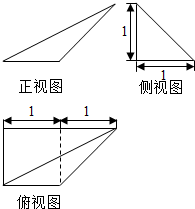
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
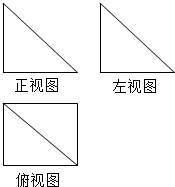 一个几何体的三视图如图所示,其中主视图和左视图是腰长为2的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )
一个几何体的三视图如图所示,其中主视图和左视图是腰长为2的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )| A. | 32$\sqrt{3}$π | B. | 4$\sqrt{3}$π | C. | 48π | D. | 12π |
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | 6$\sqrt{6}$ | D. | $\frac{\sqrt{3}}{3}$ |
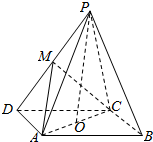 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.