题目内容
4.“a≤-1”是“函数f(x)=|(ax-1)x|在区间(0,+∞)上单调递增”的充分不必要条件.(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”)
分析 函数f(x)=|(ax-1)x|,x∈(0,+∞).当a≤-1,f(x)=-(ax-1)x=-a$(x-\frac{1}{2a})^{2}$+$\frac{1}{4a}$,可得函数f(x)在区间$(\frac{1}{2a},+∞)$上单调递增,反之不成立.
解答 解:函数f(x)=|(ax-1)x|,x∈(0,+∞).
当a≤-1,f(x)=-(ax-1)x=-a$(x-\frac{1}{2a})^{2}$+$\frac{1}{4a}$,
∴函数f(x)在区间$(\frac{1}{2a},+∞)$上单调递增,反之不成立,例如取a=-$\frac{1}{2}$时,同样可得函数f(x)在区间$(\frac{1}{2a},+∞)$上单调递增,
∴“a≤-1”是“函数f(x)=|(ax-1)x|在区间(0,+∞)上单调递增”的充分不必要条件.
故答案为:充分不必要.
点评 本题考查了函数的单调性、充要条件的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.下列函数是奇函数的是( )
| A. | y=xsinx | B. | y=x2cosx | C. | y=$\frac{sinx}{x}$ | D. | y=$\frac{cosx}{x}$ |
15.记max{a,b}表示a,b中较大的数,则函数f(x)=x•max{-$\frac{lnx}{ln2}$,4x2}(x>0)的递增区间为( )
| A. | (0,e) | B. | (0,$\frac{1}{e}$) | C. | (0,$\frac{1}{e}$),($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$),(e,+∞) |
19.已知四棱锥P-ABCD为球O内接四棱锥,PC⊥平面ABCD,PC=$\sqrt{6}$,AD=$\frac{1}{2}$AB=2,∠DAB=$\frac{π}{3}$,则球O的表面积S=10π.
16.在△ABC中,已知a=$\sqrt{2}$,c=1,A=45°,则sinC等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{4}$ | D. | 1 |
13.过曲线y=$\sqrt{x}$上的点(4,2)的切线方程是( )
| A. | x+4y+4=0 | B. | x-4y-4=0 | C. | x-4y+4=0 | D. | x+4y-4=0 |
1.某多面体的三视图如图所示,则该多面体各面的面积中最大的是( )
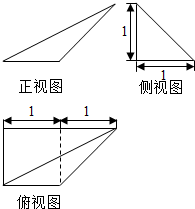

| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |