题目内容
13．若A点坐标为（1，1），F1是椭圆5x2+9y2=45的左焦点，点P是该椭圆上的动点，则|PA|+|PF1|的最大值为（ ）| A． | $6-\sqrt{2}$ | B． | $6+\sqrt{2}$ | C． | $5+\sqrt{2}$ | D． | $7+\sqrt{2}$ |
分析 求得椭圆的标准方程，可得a=3，|PF1|+|PF2|=2a=6，|PF1|=6-|PF2|，所以|PF1|+|PA|=6-|PF2|+|PA|=6+（|PA|-|PF2|），由此结合图象能求出|PF1|+|PA|的最大值．
解答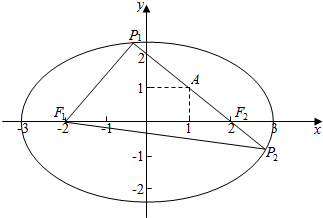 
解：椭圆5x2+9y2=45即为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1，
可得a=3，b=$\sqrt{5}$，c=2，
∵|PF1|+|PF2|=2a=6，
那么|PF1|=6-|PF2|，
所以|PF1|+|PA|=6-|PF2|+|PA|
=6+（|PA|-|PF2|）
根据三角形三边关系可知，
当点P位于P2时，|PA|-|PF2|的差最大，
此时F2与A点连线交椭圆于P2，
易得|AF2|=$\sqrt{2}$，
此时，|PF1|+|PA|也得到最大值，其值为6+$\sqrt{2}$．
故选：B．
点评 本题考查椭圆的大定义、方程和性质和应用，解题时要注意数形结合法以及定义法的合理运用．
练习册系列答案
相关题目
16．在△ABC中，已知a=$\sqrt{2}$，c=1，A=45°，则sinC等于（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{6}}{4}$ | D． | 1 |
4．几何体的三视图如图所示，则该几何体的体积为（ ）
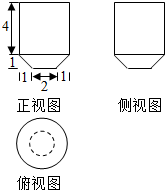
| A． | $\frac{53}{3}$π | B． | $\frac{55}{3}$π | C． | 18π | D． | $\frac{76}{3}$π |
1．某多面体的三视图如图所示，则该多面体各面的面积中最大的是（ ）
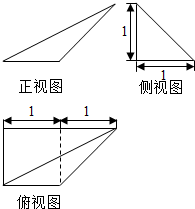
| A． | 1 | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\sqrt{5}$ |
8．
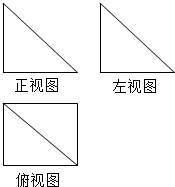一个几何体的三视图如图所示，其中主视图和左视图是腰长为2的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则该球的表面积是（ ）
一个几何体的三视图如图所示，其中主视图和左视图是腰长为2的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则该球的表面积是（ ）| A． | 32$\sqrt{3}$π | B． | 4$\sqrt{3}$π | C． | 48π | D． | 12π |
18．某几何体的三视图如图所示，则该几何体的外接球表面积为（ ）
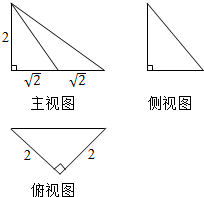
| A． | 4$\sqrt{3}$π | B． | 12π | C． | 24π | D． | 48π |
5．表面积为40π的球面上有四点S、A、B、C且△SAB是等边三角形，球心O到平面SAB的距离为$\sqrt{2}$，若平面SAB⊥平面ABC，则三棱锥S-ABC体积的最大值为（ ）
| A． | 2 | B． | $\frac{2\sqrt{3}}{3}$ | C． | 6$\sqrt{6}$ | D． | $\frac{\sqrt{3}}{3}$ |
2．若椭圆$\frac{x^2}{4}+\frac{y^2}{m}=1$的离心率$e=\frac{{\sqrt{3}}}{2}$，则实数m的值是（ ）
| A． | 1 | B． | 1或16 | C． | $\frac{4}{3}$ | D． | 16 |