题目内容
11.已知函数f(x)=$\frac{1-x}{1+{x}^{2}}$ex,求f(x)的单调区间.分析 先求出函数的导数,得到f′(x)<0,从而判断出函数的单调性.
解答 解:f′(x)=($\frac{1-x}{1+{x}^{2}}$)′ex+($\frac{1-x}{1+{x}^{2}}$)ex
=$\frac{-1{-x}^{2}-(2x-{2x}^{2})}{{(1{+x}^{2})}^{2}}$•ex+$\frac{1-x}{1{+x}^{2}}$•ex
=-xex$\frac{{(x}^{2}-2x+3)}{{(1{+x}^{2})}^{2}}$<0,
∴x<0时,f′(x)>0,f(x)递增,
x>0时,f′(x)<0,f(x)递减.
点评 本题考察了导数的应用,考察函数的单调性问题,是一道基础题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
1.某多面体的三视图如图所示,则该多面体各面的面积中最大的是( )
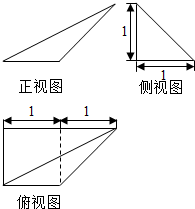

| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
2.若椭圆$\frac{x^2}{4}+\frac{y^2}{m}=1$的离心率$e=\frac{{\sqrt{3}}}{2}$,则实数m的值是( )
| A. | 1 | B. | 1或16 | C. | $\frac{4}{3}$ | D. | 16 |
16.某三棱锥的三视图如图所示,该三棱锥的表面积是( )
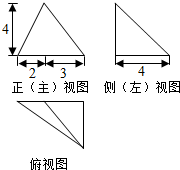

| A. | 56+12$\sqrt{5}$ | B. | 60+12$\sqrt{5}$ | C. | 30+6$\sqrt{5}$ | D. | 28+6$\sqrt{5}$ |
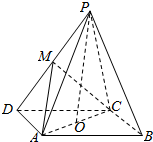 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.