题目内容
12.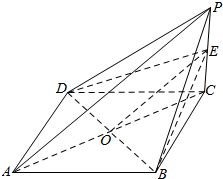 如图所示,在四棱锥P-ABCD中,四边形ABCD是边长为2的正方形,平面ABCD⊥平面PCD,∠PCD=90°,PC=1.5,E是侧棱PC上的动点.
如图所示,在四棱锥P-ABCD中,四边形ABCD是边长为2的正方形,平面ABCD⊥平面PCD,∠PCD=90°,PC=1.5,E是侧棱PC上的动点.(1)求证:PC⊥平面ABCD;
(2)求四棱锥P-ABCD的体积;
(3)当点E在何位置时,PA∥平面BDE?证明你的结论.
分析 (1)由面面垂直的性质可证明结论;
(2)代入棱锥的体积公式计算可求出棱锥的体积;
(3)连结AC交BD于O,连结OE,则O是BD的中点,显然当E为PC中点时,有PA∥OE,从而PA∥平面BDE.
解答 证明:(1)∵∠PCD=90°,∴PC⊥CD,
∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,PC?平面PCD,
∴PC⊥平面ABCD.
(2)V棱锥P-ABCD=$\frac{1}{3}$S正方形ABCD•PC=$\frac{1}{3}×{2}^{2}×1.5$=2.
(3)当E为PC的中点时,PA∥平面BDE.证明如下:
连结AC交BD于O,连结OE,
∵四边形ABCD是正方形,∴O是AC的中点,∵E是PC的中点,
∴OE∥PA,∵PA?平面BDE,OE?平面BDE,
∴PA∥平面BDE.
点评 本题考查了线面垂直的判定,线面平行的判定,空间几何体的体积计算,是基础题.

练习册系列答案
相关题目
15.记max{a,b}表示a,b中较大的数,则函数f(x)=x•max{-$\frac{lnx}{ln2}$,4x2}(x>0)的递增区间为( )
| A. | (0,e) | B. | (0,$\frac{1}{e}$) | C. | (0,$\frac{1}{e}$),($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$),(e,+∞) |
16.在△ABC中,已知a=$\sqrt{2}$,c=1,A=45°,则sinC等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{4}$ | D. | 1 |
13.过曲线y=$\sqrt{x}$上的点(4,2)的切线方程是( )
| A. | x+4y+4=0 | B. | x-4y-4=0 | C. | x-4y+4=0 | D. | x+4y-4=0 |
4.几何体的三视图如图所示,则该几何体的体积为( )
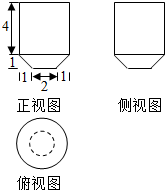

| A. | $\frac{53}{3}$π | B. | $\frac{55}{3}$π | C. | 18π | D. | $\frac{76}{3}$π |
1.某多面体的三视图如图所示,则该多面体各面的面积中最大的是( )
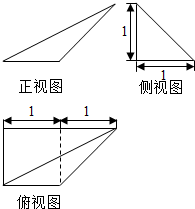

| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
2.若椭圆$\frac{x^2}{4}+\frac{y^2}{m}=1$的离心率$e=\frac{{\sqrt{3}}}{2}$,则实数m的值是( )
| A. | 1 | B. | 1或16 | C. | $\frac{4}{3}$ | D. | 16 |