题目内容
6.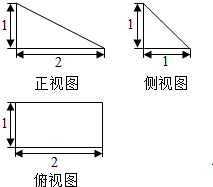 某几何体的正视图、侧(左)视图、俯视图如图所示,若该几何体各个顶点在同一个球面上,则该球体的表面积是( )
某几何体的正视图、侧(左)视图、俯视图如图所示,若该几何体各个顶点在同一个球面上,则该球体的表面积是( )| A. | 6π | B. | 12π | C. | 24π | D. | 32π |
分析 把几何体还原为长宽高分别是2、1、1的长方体,长方体的各个顶点在同一个球面上,求出球体的直径即可.
解答 解:根据题意,把几何体还原为长宽高分别是2、1、1的长方体,
则该长方体的各个顶点在同一个球面上,
该球体的直径是(2R)2=22+12+12=6
所以该球体的表面积是π(2R)2=6π.
故选:A.
点评 本题考查了利用三视图求几何体外接球表面积的应用问题,解题的关键是把几何体还原成长方体,是基础题目.

练习册系列答案
相关题目
1.某多面体的三视图如图所示,则该多面体各面的面积中最大的是( )
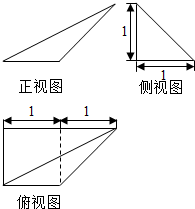

| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
11.已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示,则该正三棱锥侧视图的面积是( )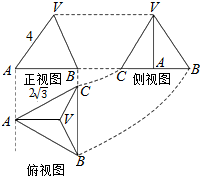

| A. | $\sqrt{39}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 6 |
18.某几何体的三视图如图所示,则该几何体的外接球表面积为( )
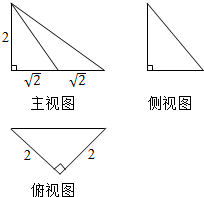

| A. | 4$\sqrt{3}$π | B. | 12π | C. | 24π | D. | 48π |
16.某三棱锥的三视图如图所示,该三棱锥的表面积是( )
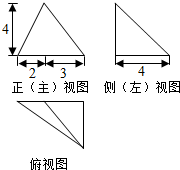

| A. | 56+12$\sqrt{5}$ | B. | 60+12$\sqrt{5}$ | C. | 30+6$\sqrt{5}$ | D. | 28+6$\sqrt{5}$ |
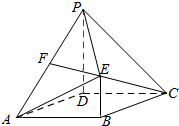 如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点.
如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点. 如图所示,在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)中,F1,F2分别是椭圆的左右焦点,点B(0,-b)是椭圆C的下顶点,BF1的延长线交椭圆C于点A,点D和点A关于x轴对称.
如图所示,在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)中,F1,F2分别是椭圆的左右焦点,点B(0,-b)是椭圆C的下顶点,BF1的延长线交椭圆C于点A,点D和点A关于x轴对称.