题目内容
已知集合A={x|x≥4或x≤-1},B=(-2,6),C={x|x<a}.
(1)求A∩B;
(2)若C⊆A,求实数a的取值范围.
(1)求A∩B;
(2)若C⊆A,求实数a的取值范围.
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:(1)借助数轴会好解一些,从而得出A∩B,
(2)由C⊆A,从而得出实数a的取值范围.
(2)由C⊆A,从而得出实数a的取值范围.
解答:
 解:(1)∵A={x|x≥4或x≤-1},B=(-2,6),
解:(1)∵A={x|x≥4或x≤-1},B=(-2,6),
∴A∩B=(-2,-1]∪[4,6).
(2)∵C⊆A,
∴a≤-1,
即a的取值范围为a≤-1.
 解:(1)∵A={x|x≥4或x≤-1},B=(-2,6),
解:(1)∵A={x|x≥4或x≤-1},B=(-2,6),∴A∩B=(-2,-1]∪[4,6).
(2)∵C⊆A,
∴a≤-1,
即a的取值范围为a≤-1.
点评:本题考查了集合的运算与集合之间的包含关系,属于基础题.

练习册系列答案
相关题目
在等差数列{an}中,若a3+2a6+a9=120,则S11等于( )
| A、330 | B、340 |
| C、360 | D、380 |
当x∈(0,2]时,函数f(x)=ax2+4(a+1)x-3在x=2处取得最大值,则a的取值范围是( )
A、-
| ||
B、a≥-
| ||
C、-
| ||
| D、a∈R |
某公司员工义务献血,在体检合格人中,O型血有10人,A型血有5人,B型血有8人,AB型血有3人,从4种血型的人中各选一人去献血,不同的选法种数为( )
| A、1200 | B、600 |
| C、300 | D、26 |
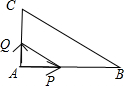 在△ABC中,∠B=30°,∠C=60°,AC=1,动点P,Q同时从A出发,沿周界运动,点P沿A→B→C;动点Q沿A→C→B运动到相遇时停止,动点Q的速度是动点P的运动速度的3倍,AP=x,△APQ的面积为y,求函数y=f(x)的解析式,并确定PQ在什么位置时S最大.
在△ABC中,∠B=30°,∠C=60°,AC=1,动点P,Q同时从A出发,沿周界运动,点P沿A→B→C;动点Q沿A→C→B运动到相遇时停止,动点Q的速度是动点P的运动速度的3倍,AP=x,△APQ的面积为y,求函数y=f(x)的解析式,并确定PQ在什么位置时S最大.