题目内容
若a,b∈R,集合{1,a+b,a}={0,
,b},则b2013-a2013= .
| b |
| a |
考点:集合的相等
专题:集合
分析:根据集合{1,a+b,a}={0,
,b},可得a≠0,a+b=0,b=1,a=
,解出即可.
| b |
| a |
| b |
| a |
解答:
解:∵集合{1,a+b,a}={0,
,b},∴a≠0,a+b=0,b=1,a=
,解得b=1,a=-1.
则b2013-a2013=1-(-1)=2.
故答案为:2.
| b |
| a |
| b |
| a |
则b2013-a2013=1-(-1)=2.
故答案为:2.
点评:本题考查了集合的性质、相等,考查了推理能力,属于基础题.

练习册系列答案
相关题目
给出四个条件:(1)b>0>a;(2)0>a>b;(3)a>0>b;(4)a>b>0.其中能推得
<
成立的是( )
| 1 |
| a |
| 1 |
| b |
| A、(1)(2)(3) |
| B、(2)(3)(4) |
| C、(1)(3)(4) |
| D、(1)(2)(4) |
已知f(x)=
,则f(5)的值为( )
|
| A、4 | B、6 | C、8 | D、11 |
已知:A={x|y=2x+1}、B={(x,y)|x+4y=13}.则A∩B=( )
| A、{1,3} | |||||
| B、∅ | |||||
C、{(x,y)|
| |||||
| D、{(1,3)} |
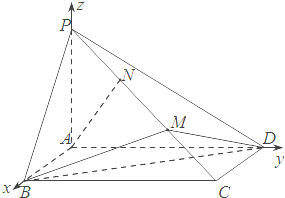 己知四棱锥P-ABCD,其中底面ABCD为矩形侧棱PA⊥底面ABCD,其中BC=2,AB=2PA=6,M,N为侧棱PC上的两个三等分点,如图所示:
己知四棱锥P-ABCD,其中底面ABCD为矩形侧棱PA⊥底面ABCD,其中BC=2,AB=2PA=6,M,N为侧棱PC上的两个三等分点,如图所示: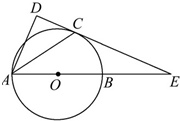 如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.